2023-6-4 arXiv: 1063 papers, small models making their own data, Way simpler RLHF, Adam accumulation
This newsletter made possible by MosaicML.
We beat last week’s record paper count, so once again we’re going to have more breadth and less depth than usual. Also a heads up that I’m more likely to make mistakes.
Impossible Distillation: from Low-Quality Model to High-Quality Dataset & Model for Summarization and Paraphrasing
They generate a high-quality task-specific dataset by iteratively:
having a model generate examples,
filtering out all but the highest-quality examples, and then
using these high-quality examples to improve the model.
An off-they-shelf model generates the examples at the start, but once they have enough data, they train a task-specific model and use that instead.
To extract high-quality samples, they bake in a bunch of task-specific logic. E.g., forcing the decoding to generate certain keywords when doing summarization. They also filter based on length, entailment, and diversity.
The final task-specific model can outperform 200x larger generalist models like GPT-3.
And the training data they generate might be even better than human-written examples.
These are important results. If we can generate high-quality training data a) in exchange for compute rather than human time, and b) with a way smaller model than ChatGPT & co, it could be a super scalable method for cranking up text model quality.
Using generative models to generate training data seems like the clearest and most independently-reproduced positive feedback loop we have in machine learning right now, and this method makes that loop a lot cheaper.
These results are also further evidence of domain-specific models’ ability to outperform much larger generalist models.
The Curse of Recursion: Training on Generated Data Makes Models Forget
Here’s a paper that sounds like it’s contradicting the previous one:
“We find that use of model-generated content in training causes
irreversible defects in the resulting models, where tails of the original content distribution disappear. We refer to this effect as model collapse.”
E.g., if you iteratively train on the output of a language models, and then use that model to generate new training data, you gradually get lower accuracy and a shift towards lower-entropy sequences.
You can easily verify that this happens in simpler settings as well.
It’s not clear that there’s an outright contradiction with the above paper though. I’m interpreting this as showing that training on LM outputs induces a bias-variance tradeoff, rather than being a free win. We can get more data this way (reducing variance), but we bias our distribution away from human-generated text. Further, if we only go through one or two rounds of model → data → model → data, as done in the previous paper, we should be able to avoid most of the bias.
This paper also suggests that using the internet as training data will become less and less effective as more and more of it becomes autogenerated—at least assuming that we want to capture the distribution of human-generated text, which…we might not? Maybe standard English, French, etc, will just become lower-perplexity over time…
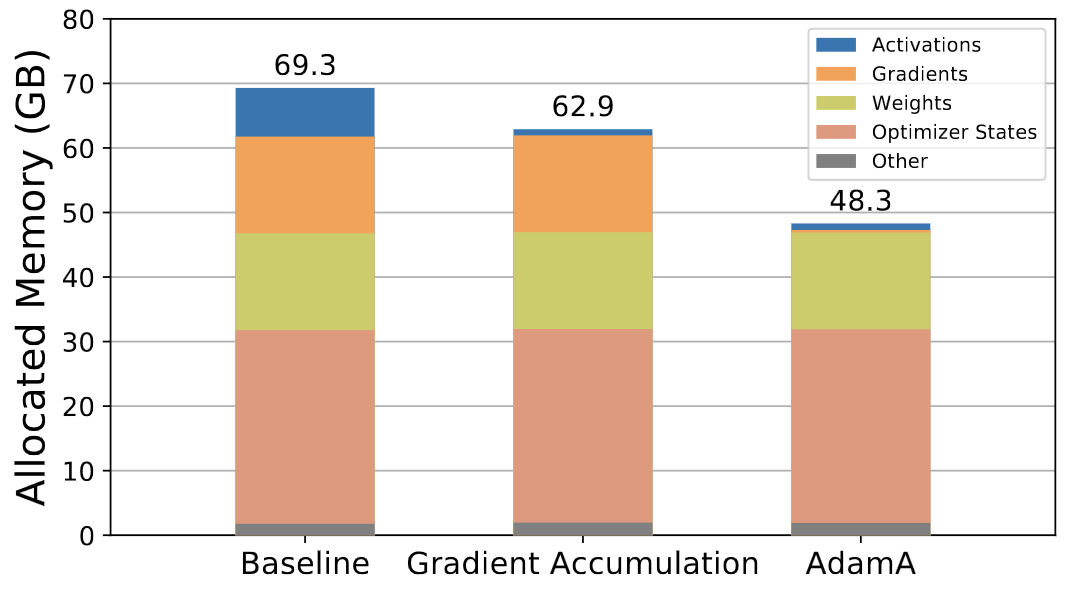
Adam Accumulation to Reduce Memory Footprints of both Activations and Gradients for Large-scale DNN Training
Alright, this is really clever. They observe that the updates you get when using Adam are a function of the momentum and RMS statistics, not the gradient itself. So you can just update the corresponding Adam state variables as soon as you compute a given gradient tensor and then free the gradient tensor instead of keeping the gradients in RAM until the start of opt.step().
This saves you basically all of the RAM that otherwise would have gone to storing gradients (probably either 2 bytes or 4 bytes per param, depending on your mixed precision settings).
This technique does break mathematical equivalence though, since you’re replacing a true average across microbatches with a moving average. But it looks like this is fine.
I really like this—just a clean, elegant idea that seems to work in practice. I’d previously thought about doing optimizer steps as a callback to eagerly free the gradients, but that couples your optimization batch size to your microbatch size; this alternative is nicer because it not only keeps these decoupled but also lets you do less work than a full optimizer step for each microbatch.
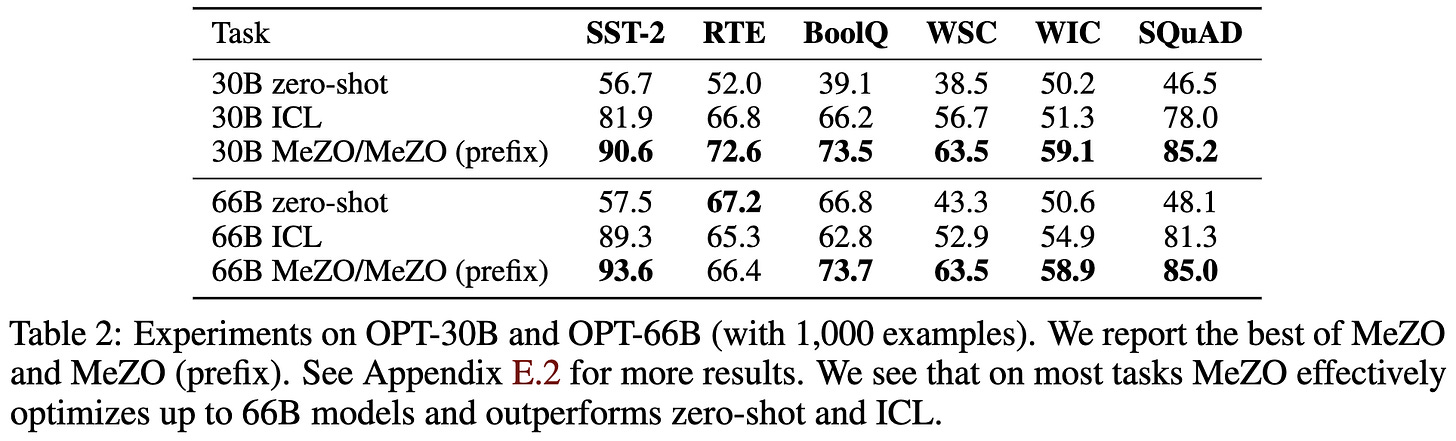
Fine-Tuning Language Models with Just Forward Passes
They actually managed to finetune some multi-billion parameter models with randomized gradient estimates instead of backward passes. The advantage of this is that it saves a lot of RAM, requiring you to materialize almost no tensors at any given time but the (perturbed) model weights.
The downside of this approach is that you get way less improvement per step. According to Appendix D.3, “all [finetuning] experiments use 1K steps and MeZO experiments use 100K steps.” This inefficiency is mostly because random perturbations tend to be almost perfectly orthogonal to the true gradient; but some of it might also stem from this method approximating raw SGD, with no momentum or anything.
If you’re willing to pay this cost, though, you can eventually get about the same accuracy.
I’m surprised they’re able to get only 100x overhead given how orthogonal random perturbations are to the gradient. Makes we wonder if we could get within 10x by, say, storing metadata across multiple perturbations to hone in on the gradient faster.
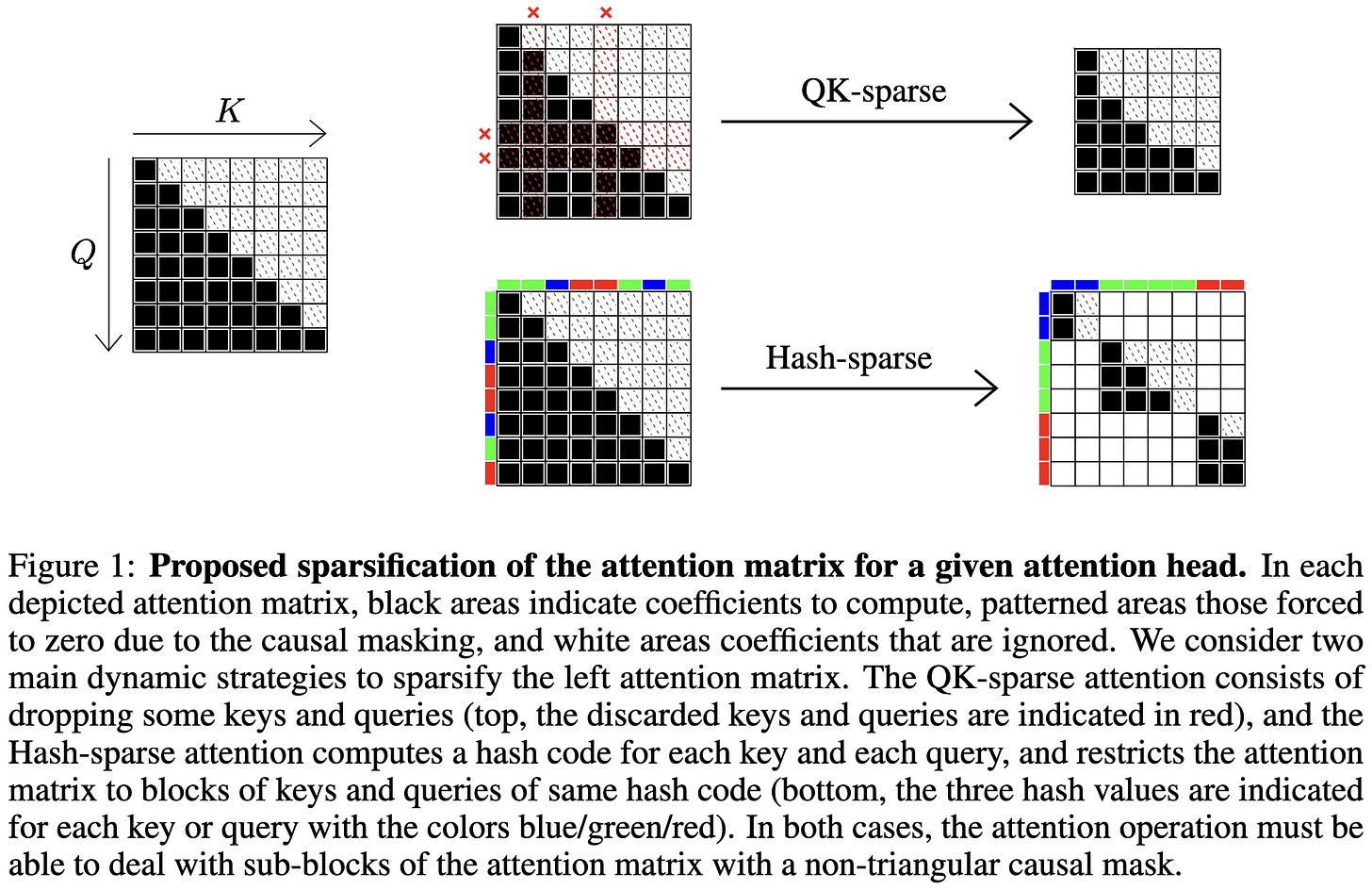
Faster Causal Attention Over Large Sequences Through Sparse Flash Attention
They wrote fast kernels for structured sparse attention matrices. The sparsity structure is either dropping rows and columns, or only computing rectangular submatrices whose rows and columns hash to the same value.
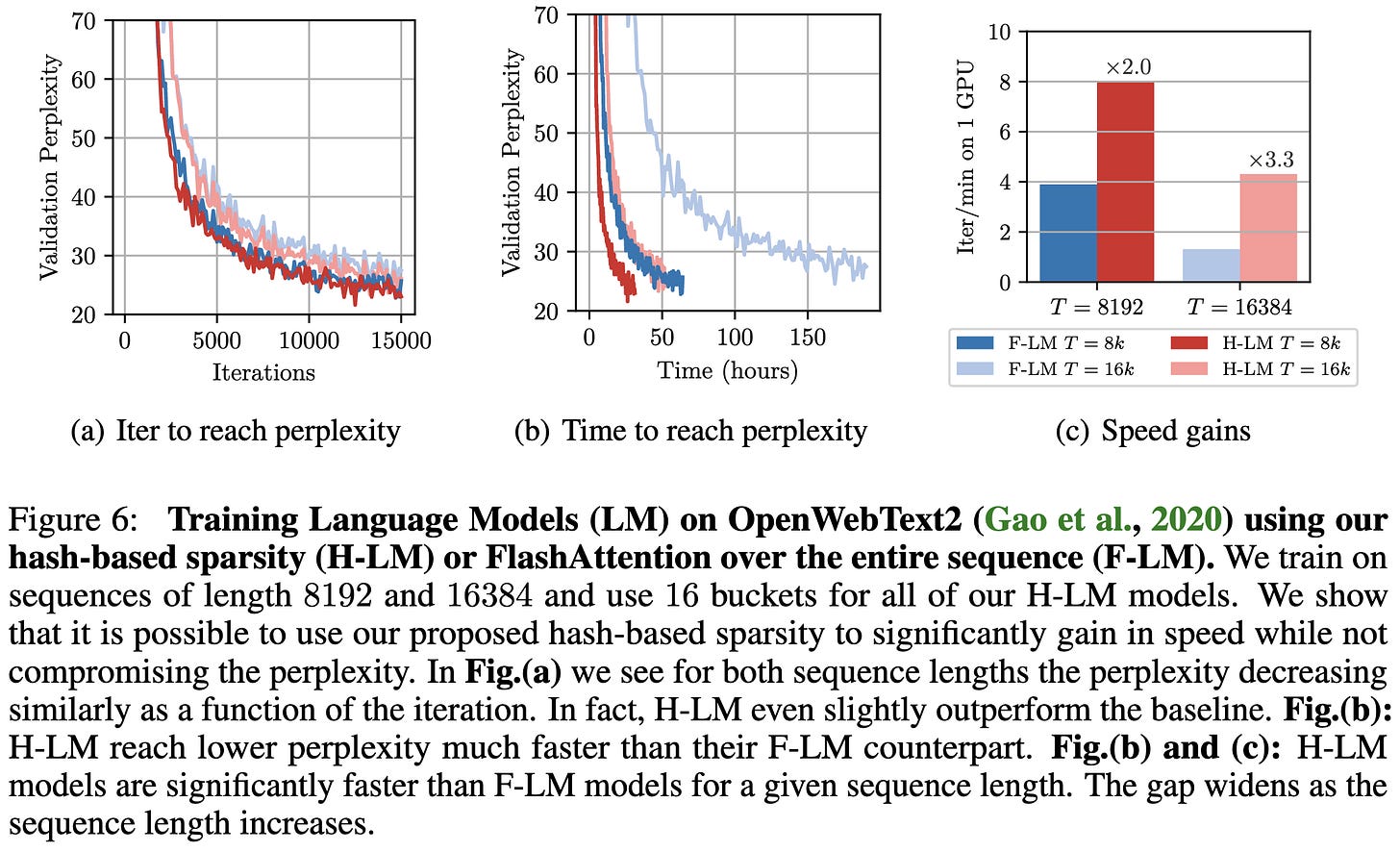
Their hash-sparse kernels are faster than dense ones starting at a sequence length of ~4k tokens.
For their query and key dropping variant, the breakeven point is at worst 16k, but can be under 2k with enough dropping.
At sequence lengths of 8k and 16k, they can get 2x faster time to perplexity than regular FlashAttention when using an appropriate hash-sparse configuration.
With query and key dropping instead of hashing, the time-to-perplexity can again be ~2x lower, though even the lowest sparsity doesn’t quite hit the same perplexity when holding steps constant.
Seems like a real, actionable improvement. Also makes me wonder if we could do better by intelligently selecting the hashing + dropping patterns. E.g., it sounds like they’re having to pad to accommodate the worst-case block, which suggests load balancing could let you sneak in extra FLOPs for free.
On the Tool Manipulation Capability of Open-source Large Language Models
What does it take to get an existing open-source model to call APIs and use the outputs?
First, we need to see how well these models do by default. The answer is…not very well. Though, interestingly, GPT-4 is great at this, suggesting that this is part of what it was trained to do.
Here’s a breakdown of how, specifically, different models fail:
To help correct these failures, they generate a bunch of examples of tool use to finetune on. The examples use human-generated templates with machine-generated arguments and outputs. They also augment models with a module that retrieves relevant examples for a given query.
Lastly, they design their prompt carefully.
To evaluate how well different tool use approaches work, they also introduce the ToolBench benchmark.
Using this benchmark, they find that their changes can make open source models much better at using tools.
The tool use literature doesn’t seem to have converged on any standard practices, but enough groups are independently doing it now that it does seem to be a real thing. Also great to have ToolBench—hopefully this will help this area standardize and make apples-to-apples comparisons.
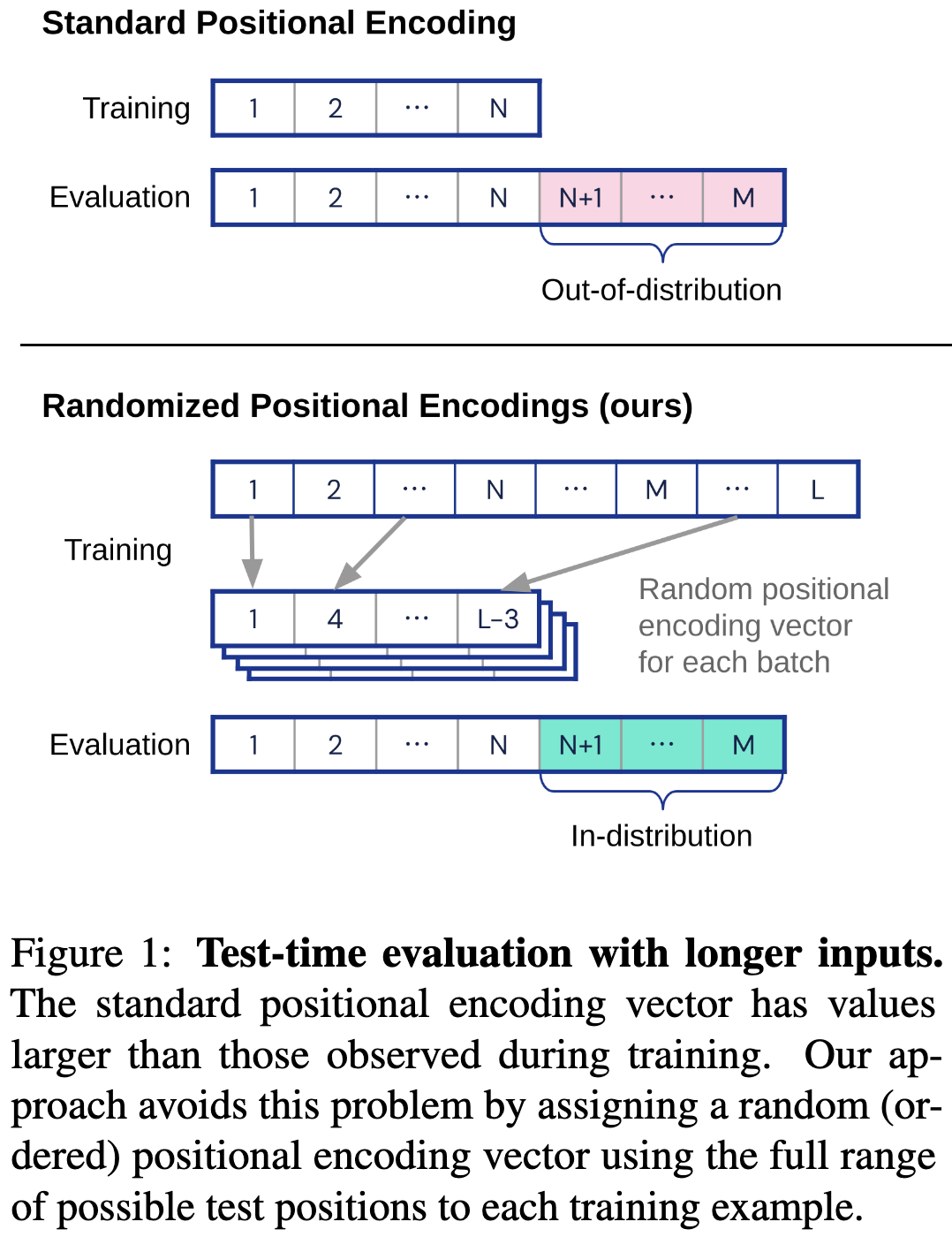
Randomized Positional Encodings Boost Length Generalization of Transformers
They propose randomly lying to your model about where it is in the sequence instead of always telling it it’s at the start. So, e.g., you might tell it that the full input is actually just the end of a super long sequence. A few notes:
The max “virtual” sequence length has to be specified ahead of time, but can be much longer than the sequences you train on.
The random positions are sampled without replacement and shared within a given batch.
The positional embeddings you feed in should be from an ordered subset of possible positions but not necessarily a contiguous one.
You can apply this idea on top of any base positional encoding scheme; e.g., you can do sin/cos embeddings, learned encodings, RoPE, etc.
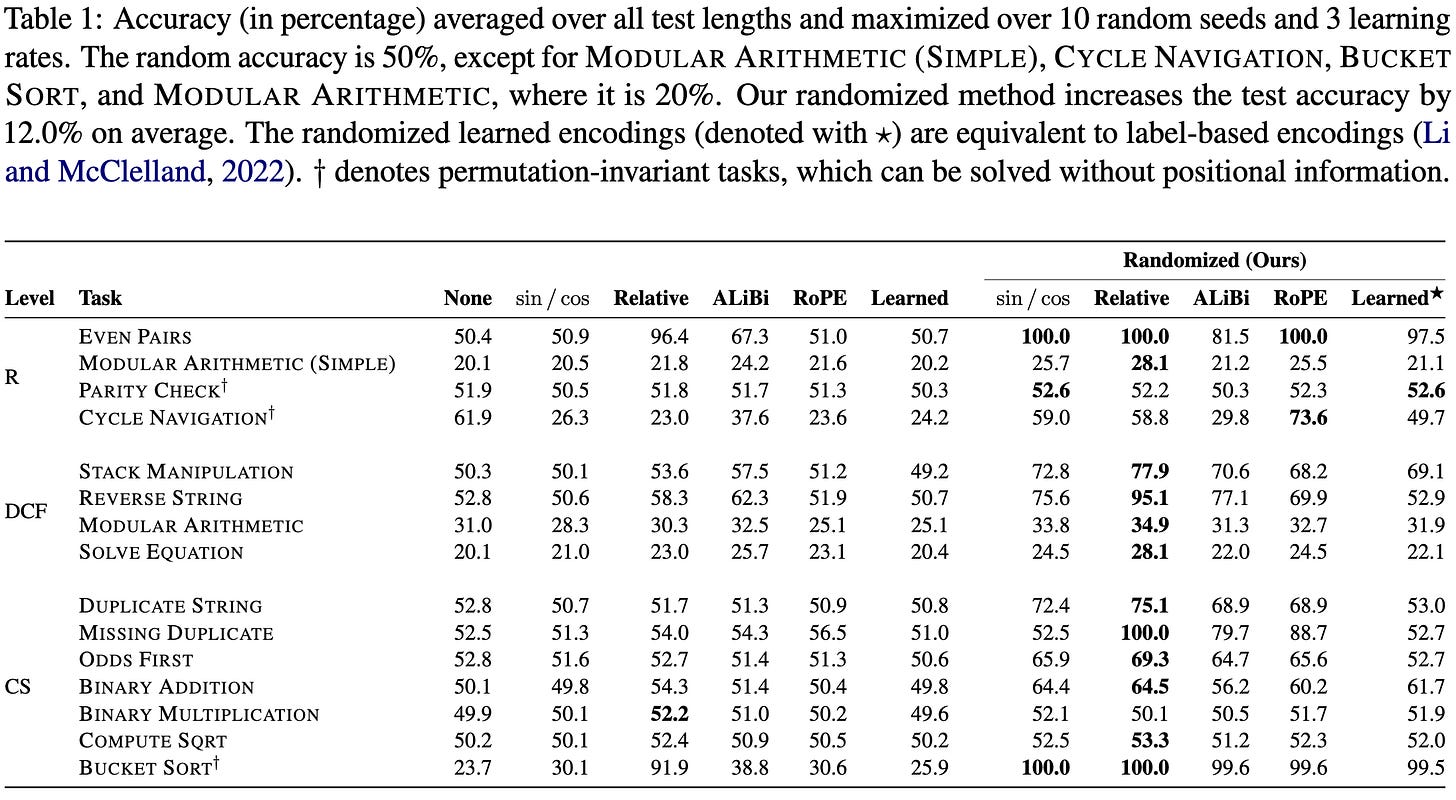
In terms of results, they find that randomized relative position encodings seem to work super well for a bunch of toy problems.
The concept seems pretty plausible given the success of randomized data augmentation methods in computer vision, but of course needs to be reproduced by different groups and on more tasks before we can be sure.
This and NoPE have me questioning whether we really know anything about how to encode positions, at least in decoder-only models. There’s also some great discussion of different people’s experiences here.
Rotational Optimizers: Simple & Robust DNN Training
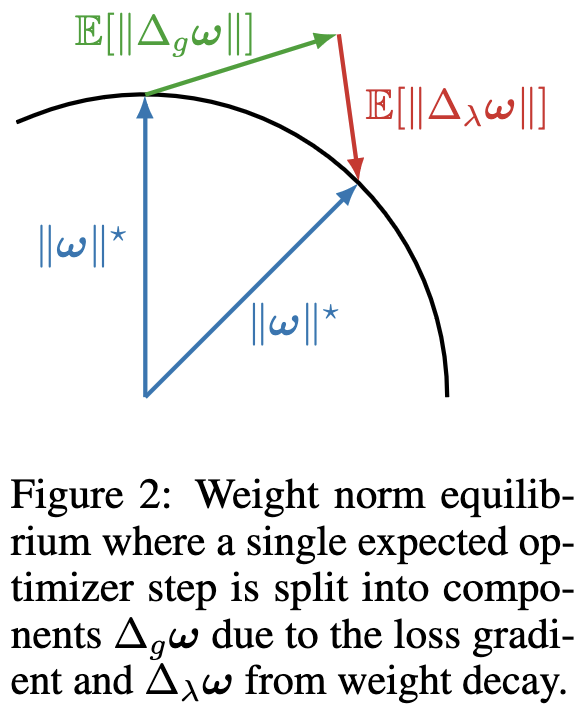
So if you didn’t happen to read this 2018 blog post, you might not have thought about how normalization and weight decay interact to drive your weights towards an equilibrium norm. This paper explains it really well:
With a normalization right after your linear op, the gradient with respect to the norm of the weights is zero.
This means your gradient is orthogonal to your weights.
This means adding an update in the gradient direction increases your weight norm, by the Pythagorean theorem.
But weight decay shrinks your weights. This combination of growing and shrinking (usually) causes your weight norm to hit some equilibrium, since the weight decay term grows linearly with the weight norm while the gradient norm (hopefully) grows sublinearly or not at all.
With an optimizer other than raw SGD, the update might not be exactly orthogonal to the weight norm. But there’s a good chance you’ll get similar dynamics.
In fact, this paper derives the equilibria you should expect to end up with using various common optimizers:
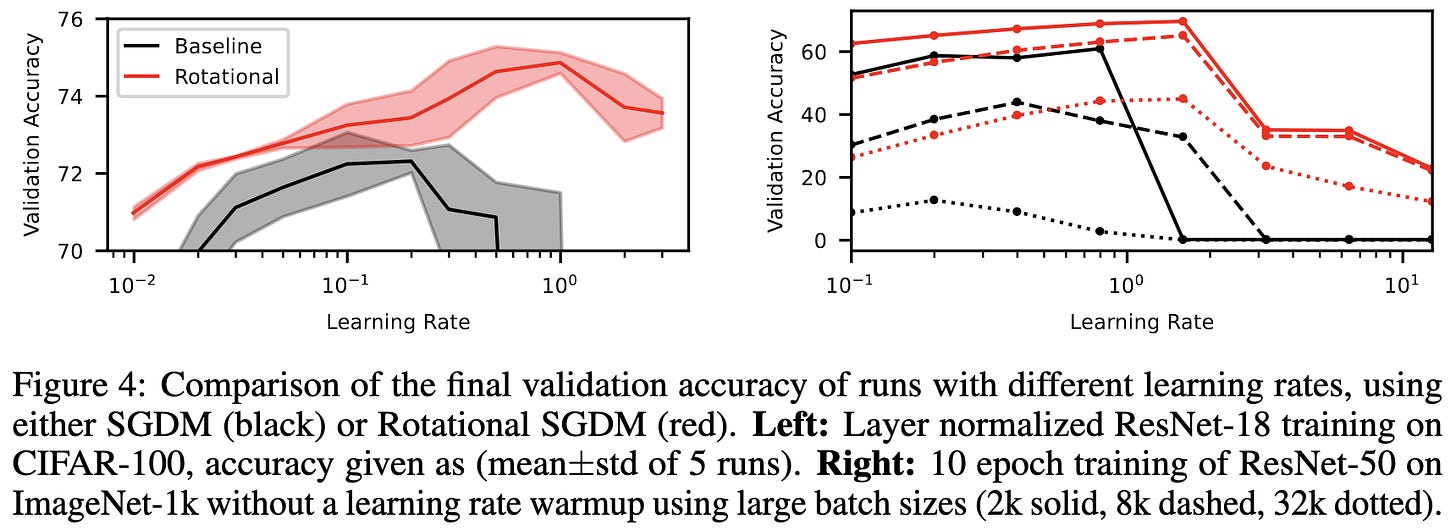
They also propose to just optimize weights such that the L2 norm stays roughly fixed directly:
Doing this seems to improve optimization and learning rate insensitivity, especially when not using warmup.
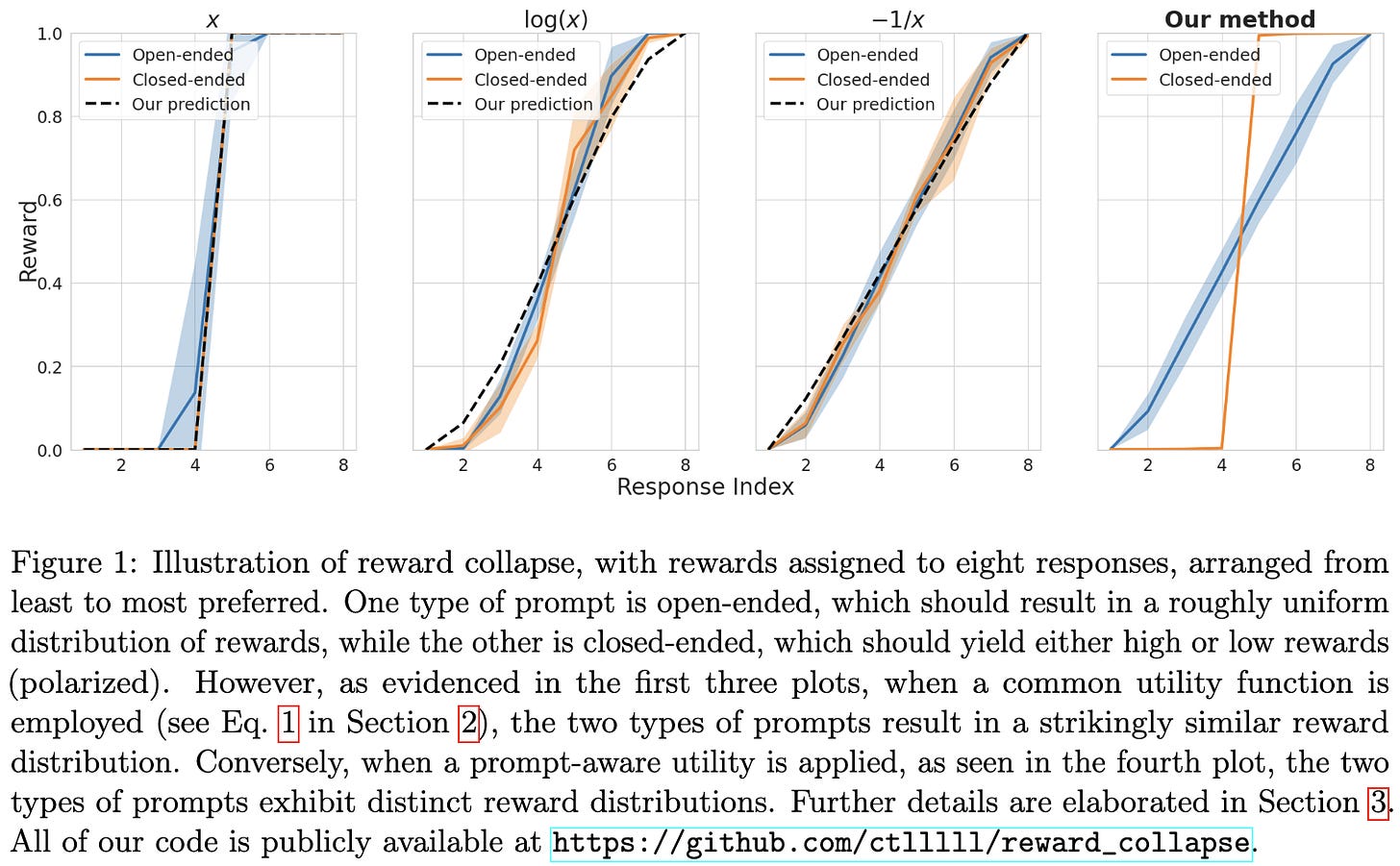
Reward Collapse in Aligning Large Language Models
Some prompts have single right answers and some have many right answers. You’d think that the distributions of RLHF-style rewards would reflect this—but it turns out they don’t. The authors propose a method to fix this that correctly gives reward for a broader array of answers in the open-ended case.
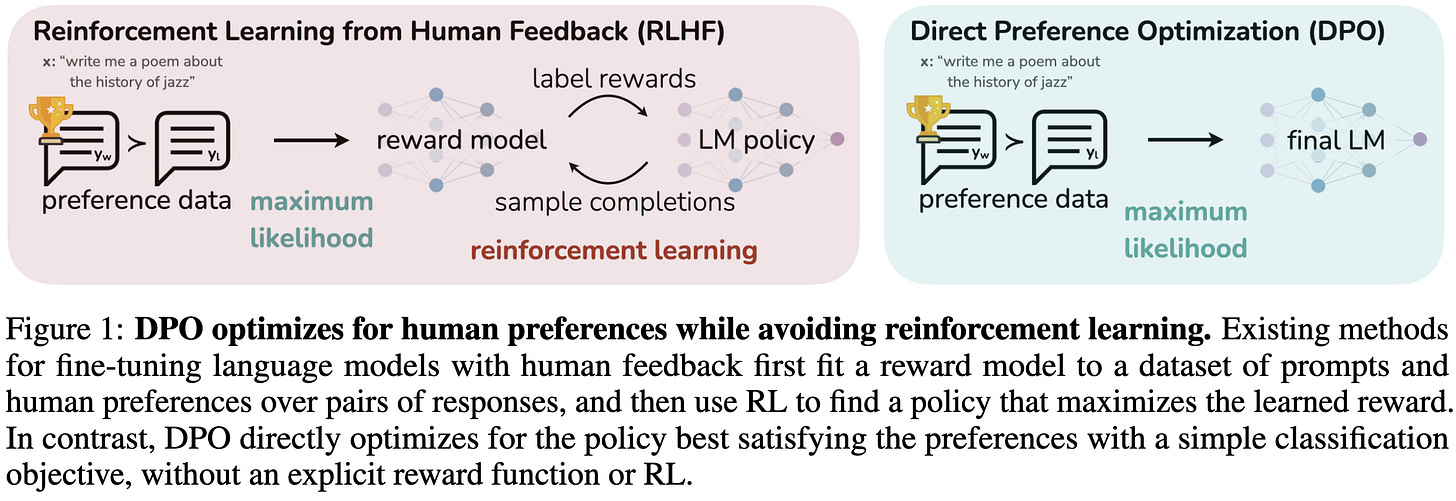
Direct Preference Optimization: Your Language Model is Secretly a Reward Model
They get the same model quality as RLHF but with a much simpler finetuning pipeline that basically just looks like training a classifier.
Instead of training a reward model and using PPO to improve the model, they just treat generation of a token as an action and optimize the policy directly. This optimization reduces to using a different loss function.
This loss function tells the model to make the good sequence more likely and the bad sequence less likely, with the gradient weighted higher when the implied reward model rates the bad one as being better.
They have a bunch of math motivating their construction and showing that it doesn’t sacrifice expressivity compared to other approaches.
Empirically, it seems to more consistently obtain high reward than alternatives.
Seems worth trying for anyone instruction-tuning text models.
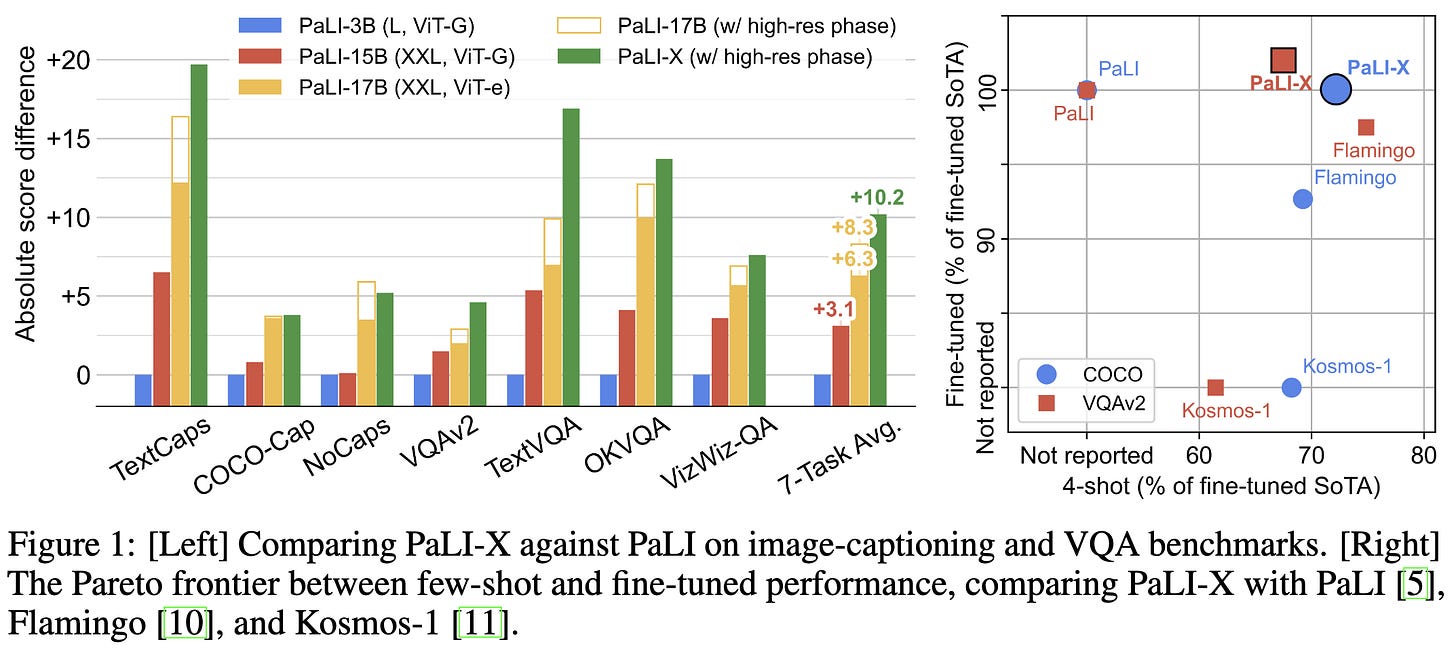
PaLI-X: On Scaling up a Multilingual Vision and Language Model
Google made a big multimodal model that can do All of the Things.
And it beats SotA on a majority of the 25 vision + language tasks they eval on.
Towards Foundation Models for Scientific Machine Learning: Characterizing Scaling and Transfer Behavior
The good news is that pretraining helps a lot for various scientific tasks, even when the pretraining and downstream tasks are pretty different.
What I’m most curious about though is whether there are clean power law scaling curves like we sometimes see for NLP.
The answer appears to be: sort of, maybe? What we’re looking for here are linear trends on a log-log plot. It looks like if you start with a pretrained model, you kind of get this linear relationship with respect to the number of finetuning examples. But if you don’t pretrain, your loss often decays faster than that.
For model size, you sort of see parallel straight lines for each model size, which is what having a typical additive error term for model size would suggest. But not really.
So I’m calling this mostly an example of power law scaling curves not being present.
Efficient Storage of Fine-Tuned Models via Low-Rank Approximation of Weight Residuals
If you’re okay with storing your finetuned weights as a compressed diff with respect to the original model, you can save a ton of storage space via a mix of adaptive factorization and quantization.
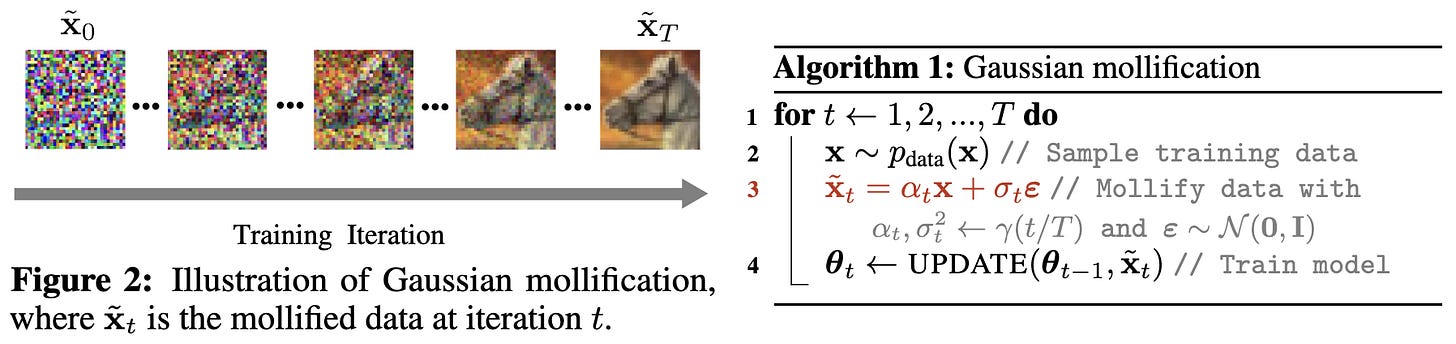
One-Line-of-Code Data Mollification Improves Optimization of Likelihood-based Generative Models
You can make VAEs and other non-diffusion models work better by just adding noise/blur to the inputs according to a schedule, somewhat like in a diffusion model.
But the schedule is over the course of training, not within decoding iterations for a single example.
This can be as simple as a one-line change to your training loop.
Might be an easy win for non-diffusion models. These results also suggest a partial explanation for the apparent success of diffusion models—namely, that noising up your inputs helps the model deal with low-probability regions of the input space.
Large Language Models Are Not Abstract Reasoners
They introduce a benchmark to measure abstract reasoning in LLMs and use it evaluate how good existing LLMs are in this respect.
Turns out they’re not too good.
White-Box Transformers via Sparse Rate Reduction
They introduce a transformer-like model in which each block has a known, mathematical function corresponding to a straightforward optimization problem.
It doesn’t seem as effective as regular transformers, but the advantage is that you know exactly what it’s doing and how it works.
Cool to see an interpretability vs quality tradeoff other than “logistic regression and decision trees are interpretable but neural nets aren’t.” I could also imagine this being extended to make deep learning much less of a black box in general.
Seems unusually interesting and definitely not yet-another-paper in any common mold. I would have spent a long time staring at this if there weren’t 1000 other papers this week…
Label Embedding by Johnson-Lindenstrauss Matrices
Why have long, one-hot label vectors when you could have short, dense ones? Label embedding isn’t a new idea but they prove some nice guarantees about it using Johnson-Lindenstrauss matrices.
Their construction often works better than other methods in practice as well.
Let's Verify Step by Step
So let’s say you want a reward model for instruction tuning. At least for mathematical reasoning, OpenAI found that it helps to provide supervision for all the reasoning steps, not just whether the final answer is right.
Supervising intermediate steps can mean something like punishing incorrect statements in a mathematical derivation.
They also released PRM800K, a dataset of human feedback you can use to train a process reward model.
Note that this the above results are a direct eval of the reward model itself (by looking at how often it assigns high reward to good answers), not an eval of whether it helps in an RLHF pipeline. Although hopefully the former is a good proxy for the latter.
Brainformers: Trading Simplicity for Efficiency
If you’re willing to make your model more complicated and your NAS more expensive, expanding your NAS search space can get you a better model.
A couple noteworthy aspects here are that a) they use few fewer attention modules, and b) it apparently matters a lot more what type of layer you use than the exact ordering of layers. E.g., you can group together blocks of MoE or FFN layers and it doesn’t matter much, but don’t replace an FFN with an attention.
Grouping MoE layers is actually super appealing because then you could eliminate almost half the all-to-alls, assuming you add some metadata to track which token is which.
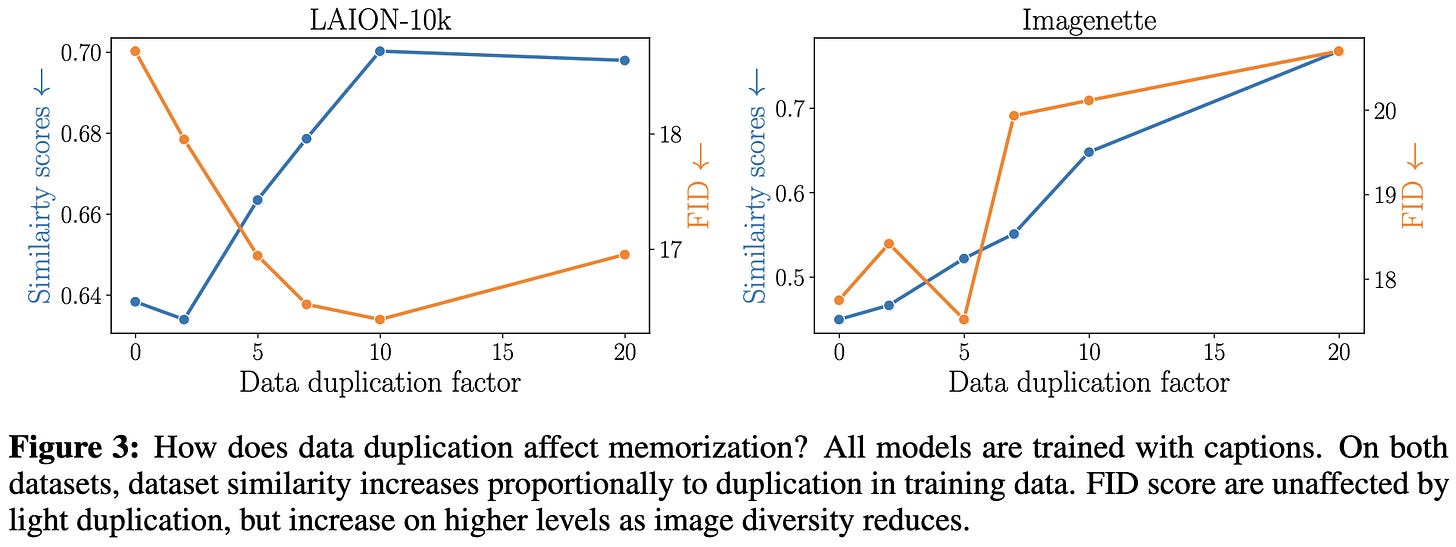
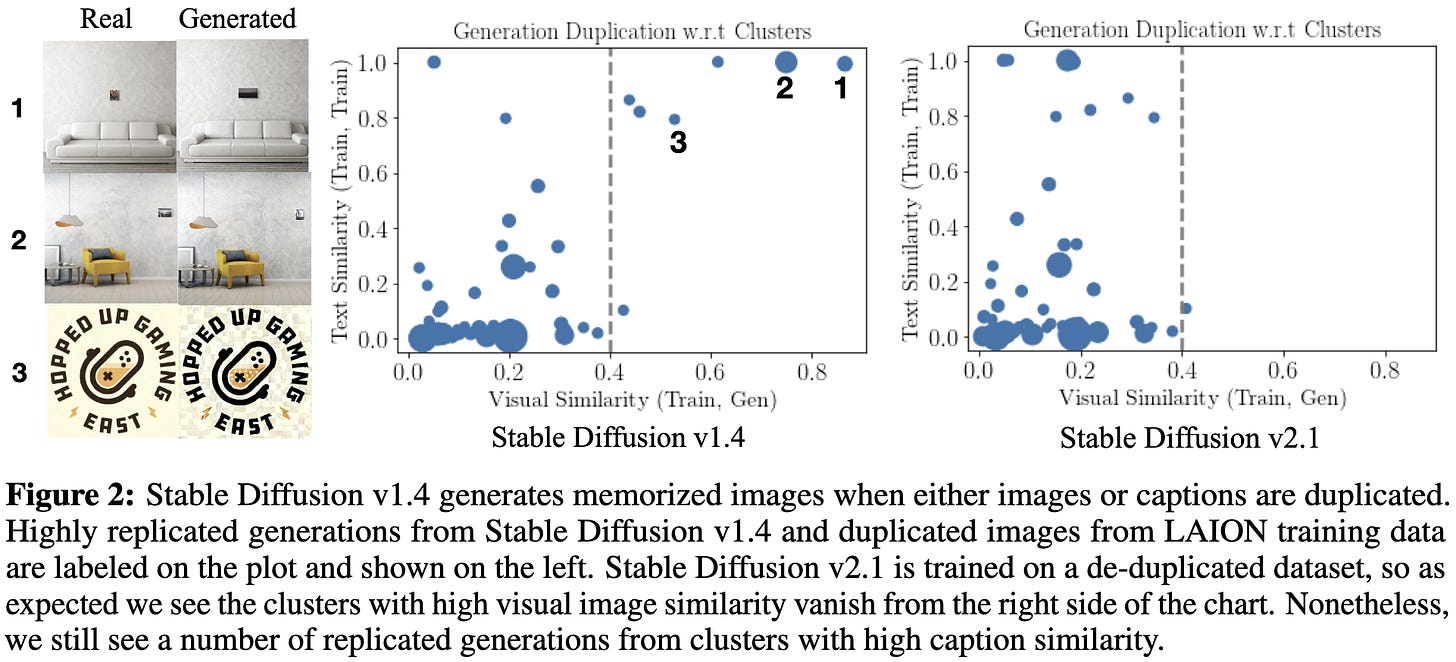
Understanding and Mitigating Copying in Diffusion Models
Sometimes diffusion models regurgitate inputs from their training data. But when does this happen?
It’s much more likely when the image or its caption shows up a lot in the training data. If you deduplicate your training set, there’s less regurgitation.
But that’s not the full story. Low-entropy images are also more likely to be simple, as measured by JPEG compressibility.
Further, having highly specific prompts that resemble particular training captions can also elicit regurgitation.
In light of these results, they recommend a number of mitigation strategies. Besides deduplicating images, you should resample/paraphrase duplicate captions and optionally just throw away generations that are too similar to training images at test time.
Improving CLIP Training with Language Rewrites
They do data augmentation for CLIP training by having language models reword the image captions.
At least in the multi-epoch regime, this seems to improve model quality significantly.
Their method of generating captions also seems to work much better than back translation and other baselines.
Intriguing Properties of Quantization at Scale
For some models, post-training quantization works great. But for others it works terribly. What’s up with that?
A few design choices can make a big difference. Basically, you want to keep your weights in a narrow range and avoid outliers. Weight decay, dropout, and gradient clipping help with this.
Using bf16 during training also seems to help compared to fp16.
Interestingly, bf16 seems to result in smaller and more consistent layernorm scales for both layernorms in each transformer block; I have no idea why this would be.
Great to see these careful experimental comparisons in a standardized setup.