2022-5-22 arXiv roundup: RankGen, Deep spectral clustering, Medical imaging pretraining
These summaries made possible by MosaicML. Come join us to push the boundaries of ML training!
⭐ RankGen: Improving Text Generation with Large Ranking Models
It’s tempting to look at this paper as yet another method to make the numbers go up. But there’s another story here that’s much more interesting.
But first, let’s talk about what they’re doing. The problem they’re solving is that sampling text from language models given a prefix often yields poor continuations. They solve this by training a reranker to take in multiple sampled sequences from the base language model and select the best one. Or they use a fancier variant where they do this recursively, beam searching to generate sequences of length L, taking the top ones, adding them to the prefix, and then repeating until sufficient text is generated.
To train the reranker, they use a contrastive loss that attempts to cluster embeddings of the prefix text and embeddings of generated sequences, while separating them from other embeddings. The “other embeddings” are either derived from sequences from the same document or sequences generated by another language model. This latter option is really interesting and brings us to why this isn’t just a higher numbers story.
What they’re effectively. doing is training a model to correct the mistakes of a separate pretrained model. So rather than getting better performance through finetuning or training a single bigger model, they decompose the text generator into components that can be trained independently.
And despite this independent training, it seems to work really well. Like, going from 69.7% → 80.7% MAUVE score with nucleus sampling. And that’s with a 1.2B param reranker on top of T5-XXL-C4, which is an 11B parameter model. So this isn’t just a model capacity increase.
What this means is that, besides just making the numbers go up a lot, this is an ML engineering story. They’ve found a new way to split up model training into multiple pieces that can be trained, improved, and maintained separately—which we need way more of from both a science and engineering perspective.
Besides the main story, their analysis section is interesting, and highlights correctable errors caused by common sampling methods.
And their model is bizarrely good at zero-shot retrieval, despite not even being trained for that. Suggests their contrastive learning approach might be useful more generally.
⭐ Deep Spectral Methods: A Surprisingly Strong Baseline for Unsupervised Semantic Segmentation and Localization
This is one of those rare papers that makes you feel like they found a hot knife to cut through the butter that is their problem. The idea here is to construct a (pixels x pixels) affinity matrix and then run a spectral clustering algorithm. With good pixel embeddings, this basically “just works”, with the clearest cluster (2nd-smallest eigenvector) consistently corresponding to the pixels associated with the main object in the image.
To construct good pixel embeddings, they use a combination of the keys in the final attention block of their ViT with pixel-space color information. Since these might be of different resolutions, they meet in the middle, upsampling the ViT embeddings and downsampling the color information. The ViT they use is a pretrained DINO-ViT-Base.
Their approach works really well for a variety of tasks, including unsupervised object localization:
…and single-object segmentation:
…and semantic segmentation:
…and, finally, image matting:
Makes me think we’ll be seeing more spectral methods in vision tasks. And I also wonder if this suggests that bringing back other classical approaches with a deep learning twist could be a fruitful avenue for future work.
Understanding Gradient Descent on Edge of Stability in Deep Learning
Analyzes two variants of gradient descent, the most relevant of which is “normalized GD”. This resembles Adam, and treats each gradient as being of unit length. They point out that, equivalently, this can be rewritten as using the regular gradient with a step-specific learning rate, scaled down by the gradient magnitude.
They show that, in the quadratic case, the gradient direction converges to the top eigenvector of the matrix in the quadratic term—i.e., oscillating along the direction of greatest curvature.
In the deep learning case, they show that the iterates should gradually move towards areas of the loss landscape with lower curvature, even as they oscillate along axes of high curvature.
One insight this gave me is that weight decay is even weirder with optimizers like Adam that normalize the gradients in some way. It basically applies L2 regularization with magnitude proportional to the inverse of your effective learning rate, and when the effective learning rate is getting reduced by the gradient norm, you can get an arbitrarily large L2 coefficient as your gradient norms approach zero.
Foundation Posteriors for Approximate Probabilistic Inference
Normally in a probabilistic program, you use some mix of variational inference, MCMC, etc, to try to infer posterior distributions for unknown variables given the values of observed variables. What if you just trained a language model to predict distributions over unknown variables directly, given the observed variables?
Turns out this works really well, especially when you use the language model’s distribution as an initial guess and fine-tune this distribution with the true math (or at least a variational approximation). Pretty clever idea, and makes a lot of sense given how a naive initialization can be super far from the true modes.
EXACT: How to Train Your Accuracy
Proposes to directly optimize expected accuracy by making the predictions stochastic instead of by introducing a convex surrogate loss. In this setup, the model has to produce good mean and variance vectors.
Has quadratic cost in number of classes since they have to compute an integral over the resulting gaussian distribution for each prediction. But that might be fine, depending on the network and dataset. About 10% slowdown on CIFAR-10-sized models and datasets.
Results show that their method sometimes beats cross-entropy and hinge loss on small datasets. Not too compelling empirically, but did get me thinking about adding gaussian noise to predictions in order to force models to be better calibrated; I feel like there’s some elegant solution to be had here.
Neural Network Architecture Beyond Width and Depth
What if you replace individual neurons with another neural net? And what if you do this recursively up to s times for some s? Turns out this lets you get better theoretical guarantees for function approximation.
Dataset Pruning: Reducing Training Data by Examining Generalization Influence
Prune samples based on gradient and (full?) Hessian evaluated at that sample. Samples that only perturb the parameters a little bit, according to this local quadratic approximation, get removed. Can remove 20% of the data on CIFAR-10 without losing accuracy. Like almost all dataset pruning papers, it’s unclear if this is better than just training on the whole dataset for less time.
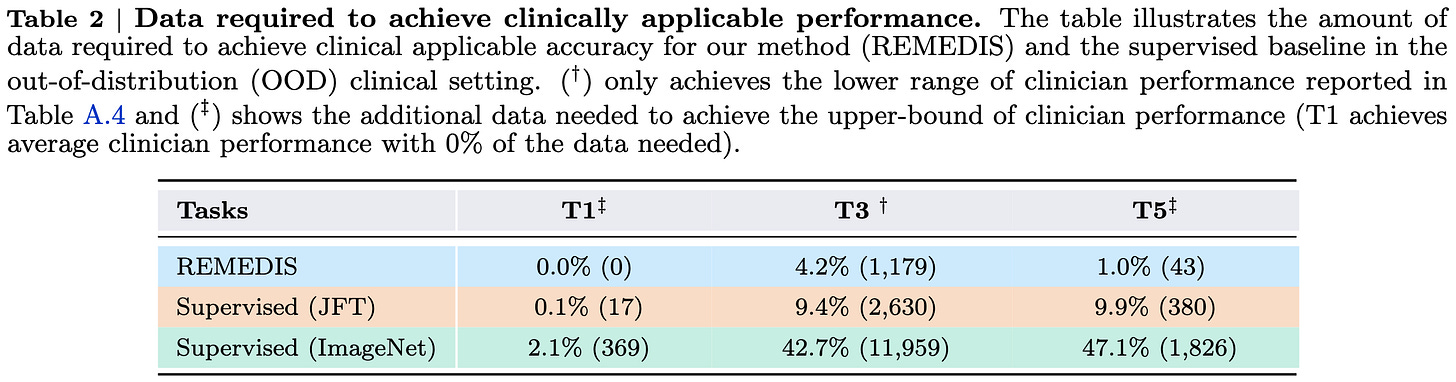
Robust and Efficient Medical Imaging with Self-Supervision
They obtain the same accuracy as specialized models using 3-100x less data. This is a big deal in medical applications, where labeled data is extremely difficult or expensive to get. The way they do this is by starting with a pretrained image classifier, doing self-supervised learning on unlabeled medical data, and then fine-tuning on a given medical task.
Encouragingly, their results are with at most a 2x-width ResNet-152 pretrained on JFT-300M and SimCLR. JFT-300M is as good as you’re going to get data-wise, but there are better alternatives to both the ResNet family and SimCLR. This suggests that these results could be improved even further.
And they already achieve human-level performance in some cases.
Overall this makes me think that the future of training is less a single pretraining stage followed by a single fine-tuning stage, and more a pipeline of jobs on progressively smaller but more task-relevant data. Especially for domains like medicine where high-quality labels are hard to come by.
Also props to the authors for the careful analysis and discussion of limitations.
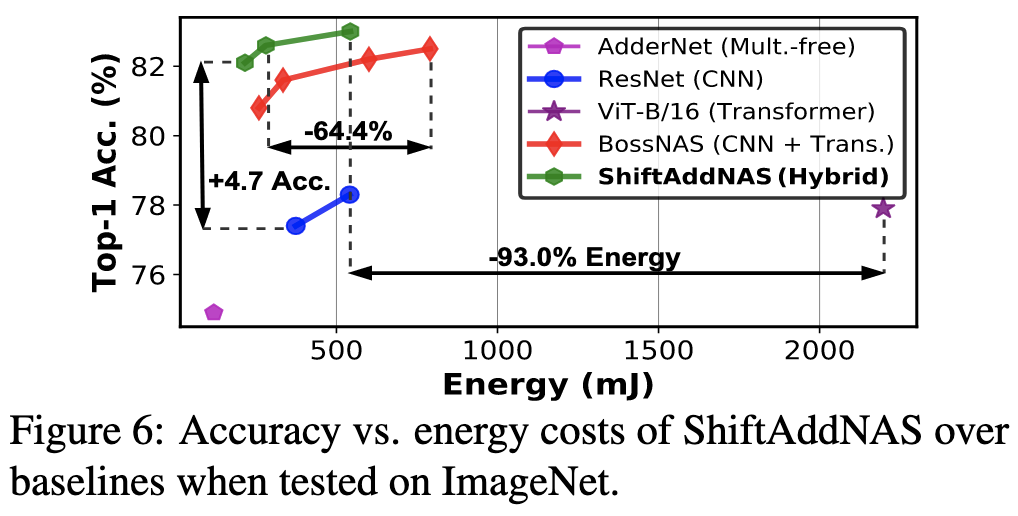
ShiftAddNAS: Hardware-Inspired Search for More Accurate and Efficient Neural Networks
Supernet-based NAS that restricts many of the weights to be powers of two. Gets unusually good results, which seems to be largely a product of choosing a good supernet. Adds a loss term that encourages weights to either be Gaussian or Laplace distributed. Shares weights across parallel blocks of a given type (e.g., Conv) within each layer, but reparameterizes them so that Gaussian and Laplace-distributed weights can be represented the same way.
Closing the gap: Exact maximum likelihood training of generative autoencoders using invertible layers
What if instead of maximizing a lower bound on p(x) in an autoencoder, we just maximized p(x) directly?
You can do this if the mapping from your latent z to observed data x is invertible. In fact, it’s a simple change of variables; with a gaussian prior over z, your loss is just the the squared norm of z + the log determinant of the Jacobian of the inverse mapping.
But the problem is that you need z and x to have the same dimensionality if you want it invertible (unless you want to do some weird stuff with pseudoinverses). So they propose to construct a deterministic representation h(x) that’s the right dimensionality and have a deterministic and invertible function mapping h(x) to the posterior over z. So it ends up like a VAE but with no sampling and a log determinant penalty rather than a negative entropy penalty.
You’ll have to stare at this one for a while to really understand it, but it was a great overview of variational autoencoders, normalizing flows, and how to think about them.