2022-7-3 arXiv roundup: Minerva, Beating power laws, Surprising OOD linearity
This newsletter made possible by MosaicML.
⭐ Solving Quantitative Reasoning Problems with Language Models
They finetune PaLM models on a corpus of math and scientific text and it turns out this works really well; their model, Minerva, gets a ton of questions right on high-school and even undergrad-level tests.
The finetuning data is 38.5B tokens; about half are from arXiv submissions and the other half are mostly from cleaned-up MathJax from on the web.
One subtlety here is that, to evaluate mathematical output, you can’t just compare tokens, since, e.g., you can express the same number as a fraction or a decimal. They ended up using SymPy to determine whether the output was mathematically equivalent to the correct answer.
They do few-shot evaluation on middle school, high-school, and undergraduate math and science problems. They use few-shot prompts, nucleus sampling for the decoding, and majority votes of up to 64 generated sequences.
They get state-of-the-art performance across a variety of tasks, despite having no external calculator or task-specific fine-tuning:
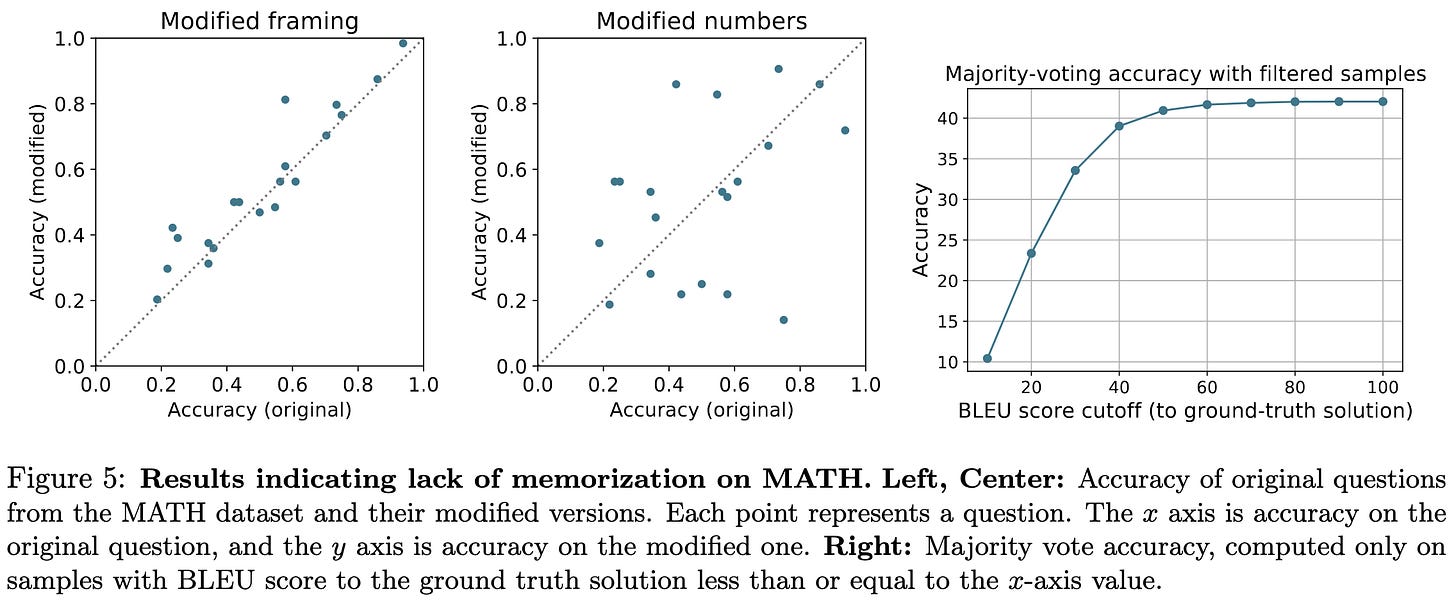
The model also doesn’t seem to just be repeating text from its training data. You can modify numbers or how the problem is worded and it still does just as well on average. It does look like the model might have high variance with respect to these details though—according to the middle plot, just changing the numbers greatly and randomly alters the probability of the model getting the right answer.
They observe that Minerva’s main failure modes are incorrect reasoning and calculation, both at small and large model sizes.
What I find most impressive about this paper is how simple the method is. There’s some problem-specific tuning, like the exact decoding / majority voting scheme, but AFAICT this is largely another datapoint suggesting that scale is (almost) all you need.
⭐ Beyond neural scaling laws: beating power law scaling via data pruning
They had me at “large-scale benchmarking study [of many data pruning methods]…on ImageNet.”’
First, they start with some theory showing that a mix of Gaussianity assumptions, a certain perceptron training setup, and data pruning can let you get exponential loss reduction with respect to the size of your chosen data subset.
From here, they move on to empirical methods + experiments motivated by their theory.
To understand what’s going on, we need to reason about three quantities: 1) the total number of samples available, 2) the number of samples we want to keep, and 3) the heuristic used to choose which samples we keep.
First, they claim that, when few samples are available or kept, you should keep easier samples. And for abundant samples available or kept, you should keep hard ones. Makes sense intuitively and they exhaustively show that this holds in small-scale experiments.
Second, they show that you can get better-than-power-law scaling in practice through intelligent data selection. And, as a key corollary, this doesn’t happen with a fixed selection heuristic—you have to adapt it based on the amount of data you have.
They also benchmark 10 heuristics for data selection and show that these mostly don’t work so well, except for “memorization” and their proposed method.
Their proposed method is to just run all the data through a pretrained self-supervised model, cluster the embeddings, and rank samples’ hardness based on distance to their centroid. This is pretty cool because it’s dirt simple and doesn’t require labels.
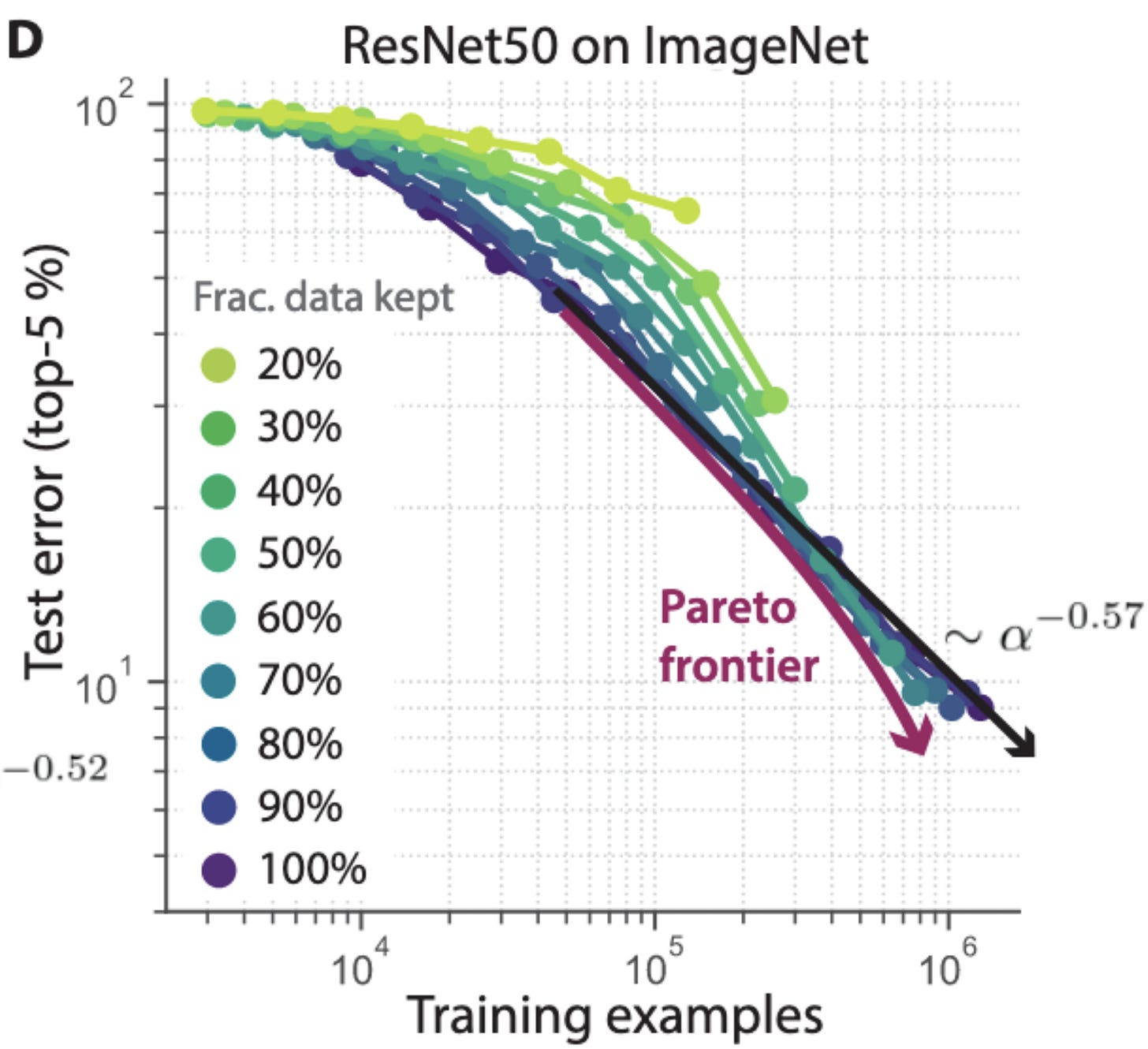
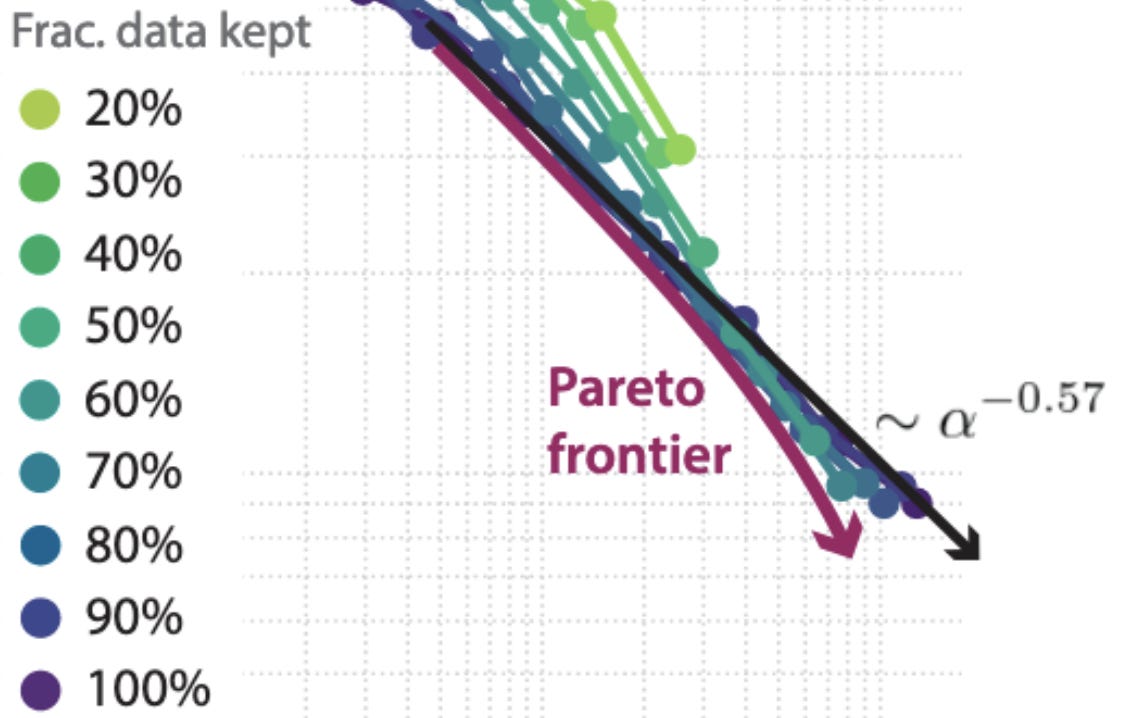
And now I’m going to be hard on this paper (because I think it’s exceptionally good, so much so that I stopped and pondered it). First, it’s not clear to me from the plots that they’re getting better-than-power-law scaling on ImageNet. The arrow they draw curves downward, but it doesn’t coincide with (and partially occludes) the measured values. (Recall that a power-law is linear on a log-log plot). See zoomed-in figure below:
I’m also not sure that we should expect power-law scaling on ImageNet to begin with; the curve for 100% data already appears to be sloping downward, and I haven’t seen prior work demonstrating power-law scaling for image classification. It would be cool to see results with their method on NLP pretraining, where we know one can often get power law scaling.
Last, I couldn’t figure out the exact method they’re using to do the data selection. I want some equation mapping total and target dataset sizes to a sampling strategy, and I don’t see that in the body of the paper. I’d similarly love an explanation of what the “memorization” baseline is, especially since it seems to be the best one.
Anyway, this was an unusually thorough and interesting paper and it makes me hopeful that we’ll be able to train models much more quickly with the right data selection.
Agreement-on-the-Line: Predicting the Performance of Neural Networks under Distribution Shift
For many models and tasks, in-distribution and out-of-distribution accuracy are linearly related. This paper finds that there often also exists a nearly-identical relationship between the agreements of two different classifiers. I.e., one can use agreement of two independent classifiers on the OOD data rather than accuracy on the OOD data.
Besides being surprising and interesting, this is practically useful: because the coefficients of the lines are so similar, one can now estimate OOD accuracy without OOD labels. Or, alternatively, one can easily discover that the linear relationship with respect to accuracy doesn’t hold for the problem in question.
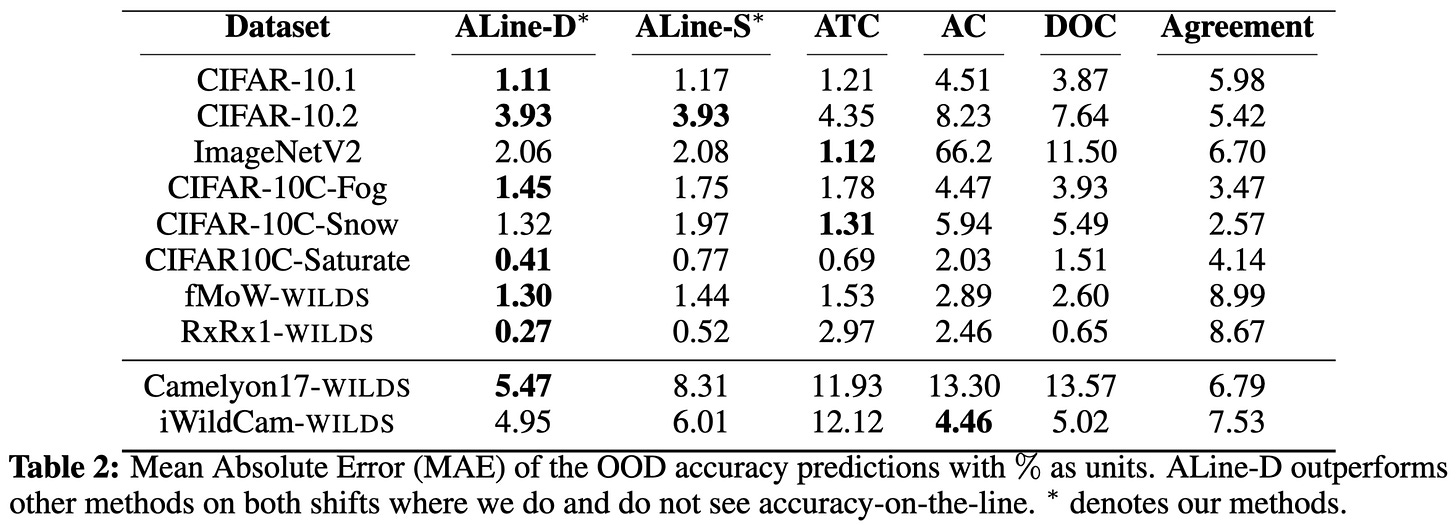
This simple linear approach often works better than existing OOD prediction methods (left two columns are the proposed methods).
Another interesting finding is that this close relationship between accuracy and agreement holds only for neural networks, and not other model families.
Papers like this are super valuable—a clear, robust, and surprising empirical finding that gives us both a practical tool and another piece of the puzzle in understanding deep learning.
Improved Text Classification via Test-Time Augmentation
Test-time augmentation is pretty common for images when you’re insensitive to latency (e.g., ensembling predictions over random crops). But what about NLP?
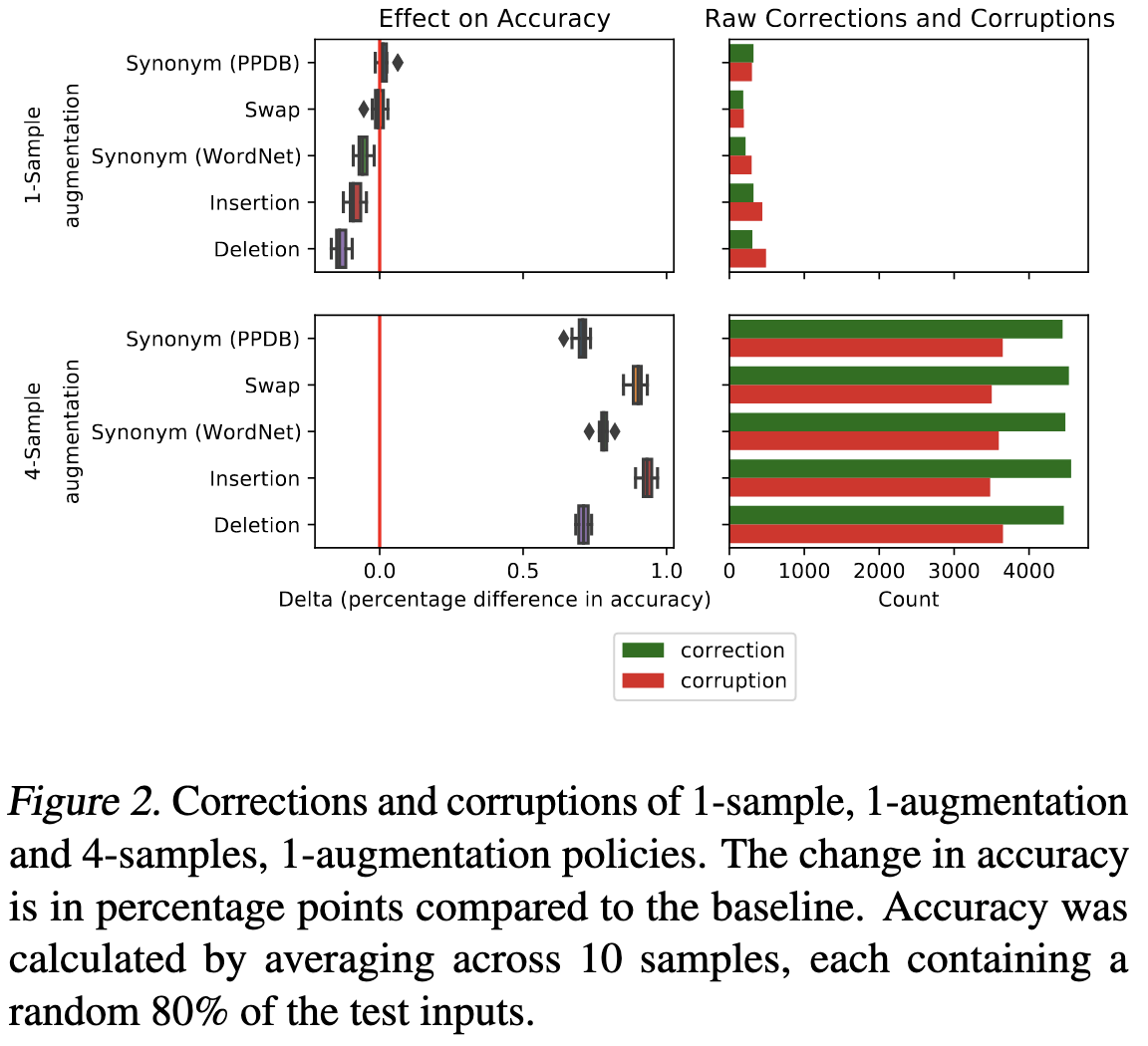
For a given input, it turns out augmentations hurt more they help—except maybe for replacement with synonyms. But if you ensemble the predictions over enough augmented copies, the errors get averaged out and you can get a small accuracy lift.
The other surprising phenomenon here is that, even for a small change in accuracy, there are a lot of changed predictions; it’s just that the correction and corruption counts are close. This is consistent with previous work, and implies that it’s all about the ratio of improved vs worsened predictions.
On the Importance of Application-Grounded Experimental Design for Evaluating Explainable ML Methods
They carry out “the most robust evaluation of post-hoc ML explanations to date” and find “no evidence of the utility of the tested methods for the task.” They frame their results as highlighting the importance of small choices in the experiment design and the need for coupling evaluation to real-world use cases.
Another entry in my Big List of ML Meta-Analyses showing that some subfield is basically just not working.
Is Power-Seeking AI an Existential Risk?
An Open Philanthropy report attempting to guesstimate probabilities of advanced AI causing terrible harm. The key claims are roughly:
It will be possible and profitable to build super-intelligent agents.
It’s hard to have a sufficiently intelligent and strategic agent that doesn’t seek power, since power is—by definition—broadly useful.
This power-seeking behavior might reach the point where it’s terrible for humanity.
The last claim seems the most controversial, and centers on humans being unable or unwilling to stop agents from doing bad things to gain more and more power. This could happen from a mix of race-to-the-bottom competition to deploy systems not known to be safe and intelligent agents deceiving us (e.g., acting nice in testing). Plus the likelihood of behavior like copying oneself on many computers being advantageous.
Skip to Section 8 (p47) for a concise walkthrough of the arguments, points in favor, and points against.
RankSEG: A Consistent Ranking-based Framework for Segmentation
Proves that segmentation based on thresholding isn’t a consistent estimator for Dice/IoU. Instead, they propose a ranking-based approach that’s grounded in theory and helps improve segmentation quality in practice.
There’s a lot going on here and you’ll have to stare at the math for a while to really get it. But the main idea is to construct a Bayes-Optimal decision rule given estimates of the pixelwise class probabilities.
They also generalize to multilabel segmentation:
Seems to help improve segmentation on fine-annotated CityScapes:
A Fast, Well-Founded Approximation to the Empirical Neural Tangent Kernel
Computing an empirical NTK can be expensive, taking up to cubic time in both the number of samples and output dimensionality. They propose the pNTK, which eliminates the output dimensionality scaling and therefore runs much faster.
Their pNTK basically amounts to summing over the logits for each sample.
Seems to be a fairly good approximation based on CIFAR-10 experiments:
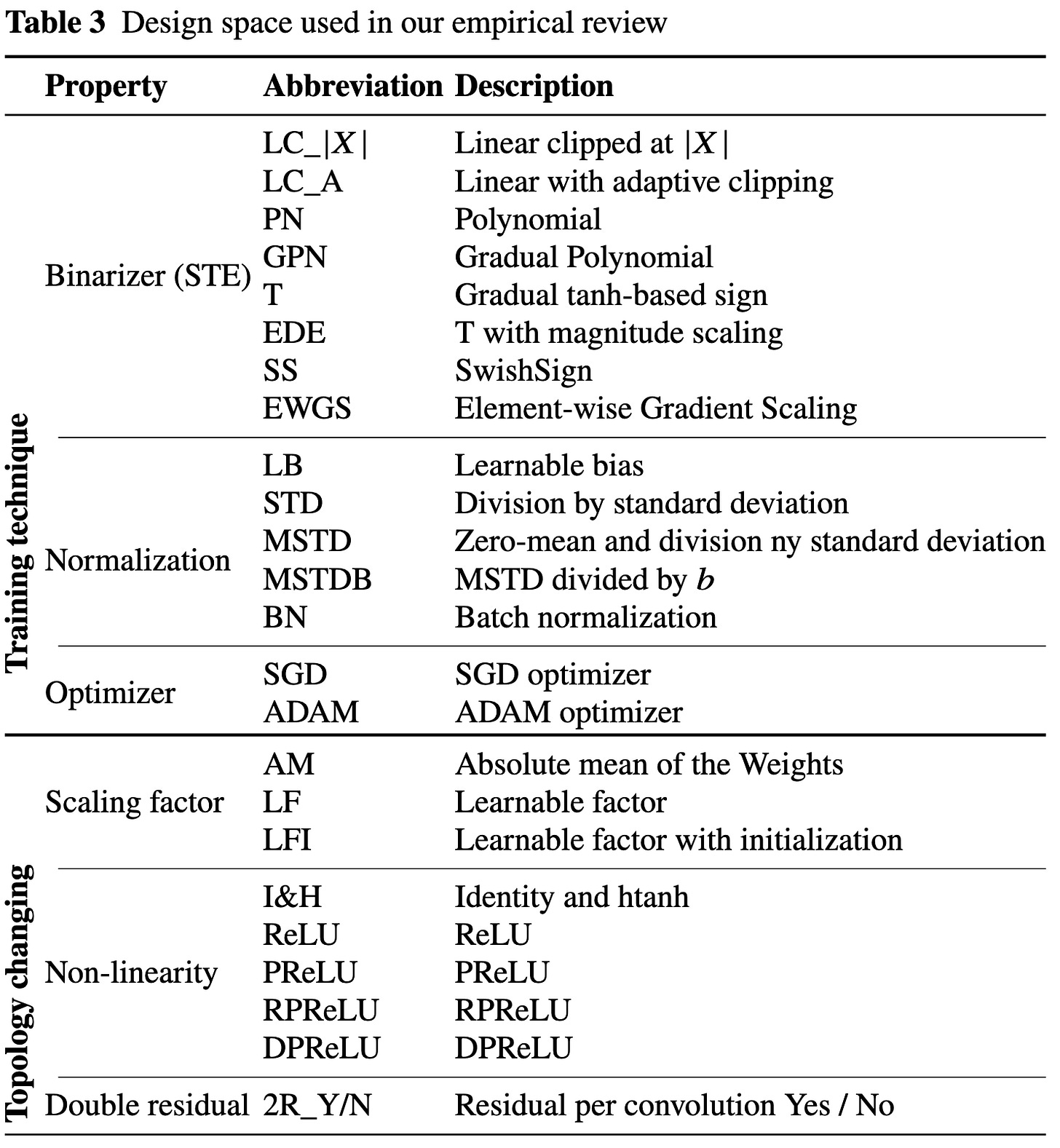
How to train accurate BNNs for embedded systems?
Systematically explores different design choices in binary neural network training. I really wish more papers were like this—asking “What choices matter for this problem?” rather than “IS MINE THE BEST? YES IT IS”.
According to ResNet + CIFAR experiments, feature normalization by standard deviation and adding more skip connections made the most significant differences (~2% and 3% accuracy lifts, respectively). They also find that applying individual changes to their baseline isn’t enough to match many published numbers; instead, one must compose together various methods to get the full accuracy.
Guillotine Regularization: Improving Deep Networks Generalization by Removing their Head
The default practice when finetuning a network on a new task is to only remove the final layer. But is removing only one layer the best choice?
In self-supervised learning, it’s already known that the answer is no—in fact, removing more layers is critical for getting good accuracy. This paper proposes viewing this practice as a generic regularization technique—Guillotine Regularization.
They find that removing more layers is helpful only if the training and downstream tasks are sufficiently different. The intuition here is that intermediate layers have more generally-useful representations, while the final layers are specialized for a particular task.
TPU-KNN: K Nearest Neighbor Search at Peak FLOP/s
New KNN library for JAX. There are two clever ideas here.
First, they generalize the roofline model to also take into account elementwise operations (“TCOPs”, with the “C” for “coordinate-wise”). This matters a lot for knn because a naive implementation will sit there searching the current list of neighbors for where to insert a closer point, plus doing at least one comparison op even when a point isn’t a neighbor.
This roofline model explains the empirical gap between searching under L2 distance vs inner product, while the traditional roofline model doesn’t:
The second clever thing they do is use a provably good randomized algorithm to avoid ever performing more than one comparison to the current neighbors. Basically, if they want K neighbors, they store a list of size L > K and only compare to one random point in the list, overwriting it if the new point is closer.
For efficiency, they just deterministically cycle through the L positions, meaning that the randomization is only with respect to data ordering; unless you have some weird seasonality in your rows with period L, this approach should be fine.
According to the numbers on two widely-used ANN benchmark datasets, their method significantly outperforms others.
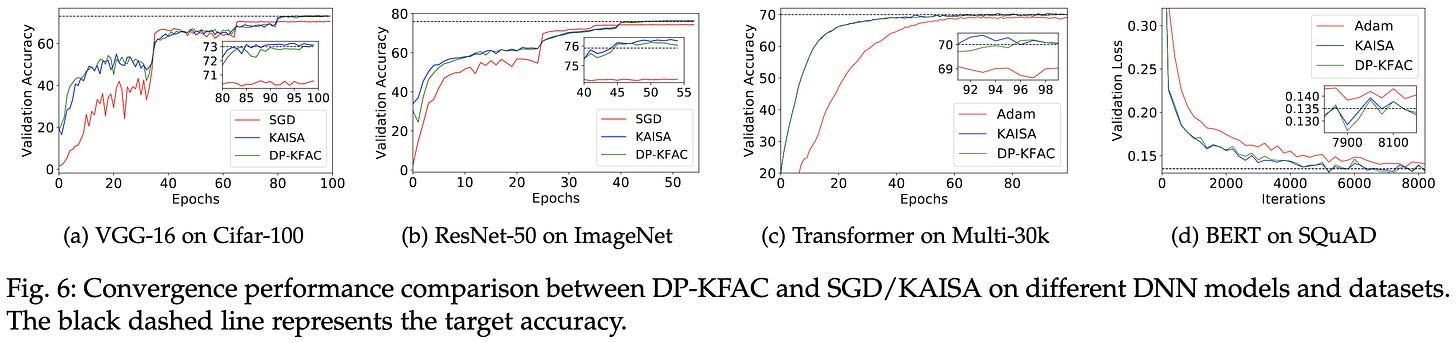
Scalable K-FAC Training for Deep Neural Networks with Distributed Preconditioning
Improved second-order optimization in PyTorch. They shard computation of the preconditioning matrices across nodes to avoid duplicate work and approximately load-balance.
Their method gets about the same training curves and final accuracy as KAISA, but runs faster.