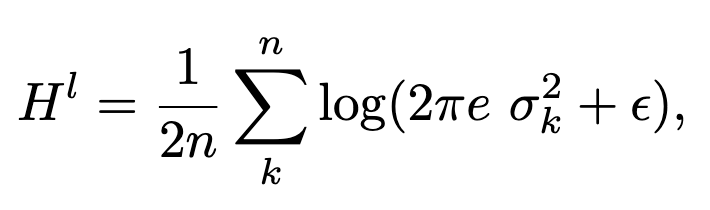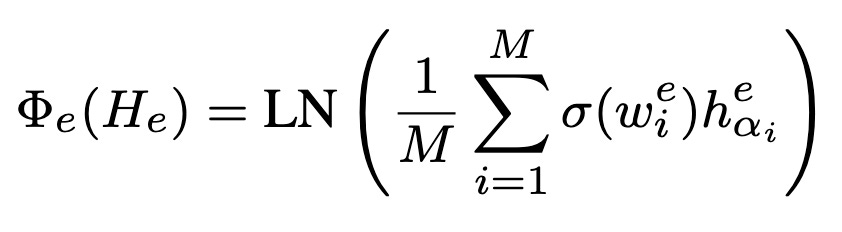2022-8-7 arXiv roundup: Adam and sharpness, Recursive self-improvement for coding, Training and model tweaks
This newsletter made possible by MosaicML.
Little bit of a slow week on arXiv, but we have some interesting science-of-deep-learning work and some actionable training tweaks.
Adaptive Gradient Methods at the Edge of Stability
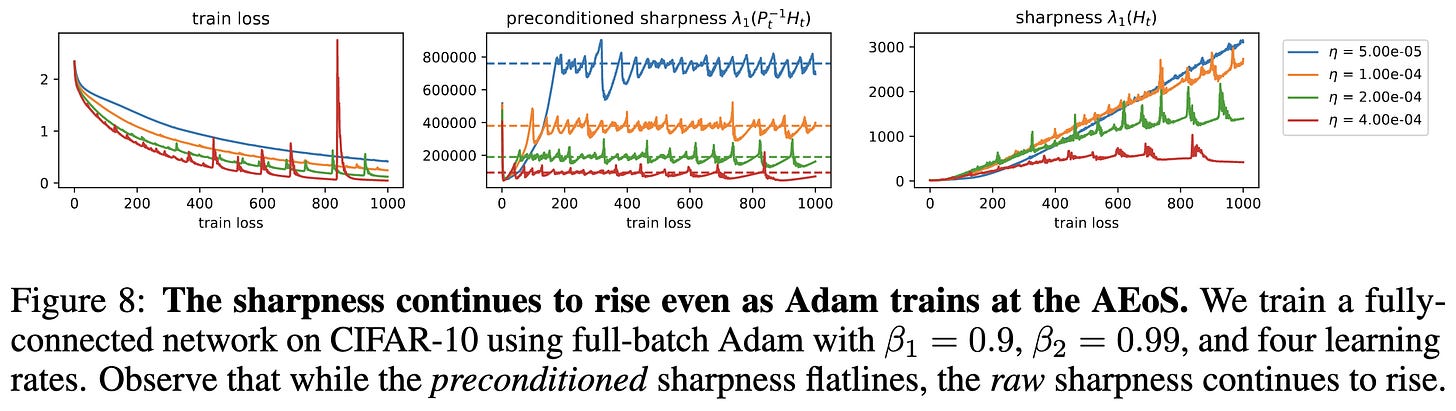
Adam doesn’t train at the edge of stability, but it does train at the edge of preconditioned stability. I.e., instead of its largest stable learning rate being limited by the largest eigenvalue of the Hessian H, it’s limited by the largest eigenvalue of the preconditioned Hessian P^(-1)H. The preconditioning here is the diagonal matrix formed by its per-parameter multipliers.
This phenomenon results in Adam finding sharper solutions than SGD when measured using the not-preconditioned Hessian.
Relatedly, the sharpness of Adam’s solution increases over time, even as the preconditioned sharpness plateaus. This indicates that the preconditioning is gradually adapting to the local curvature.
When trained with smaller batches and larger learning rates, Adam finds solutions with lower preconditioned sharpness. This is consistent with previous results indicating that both of these help find flatter minima.
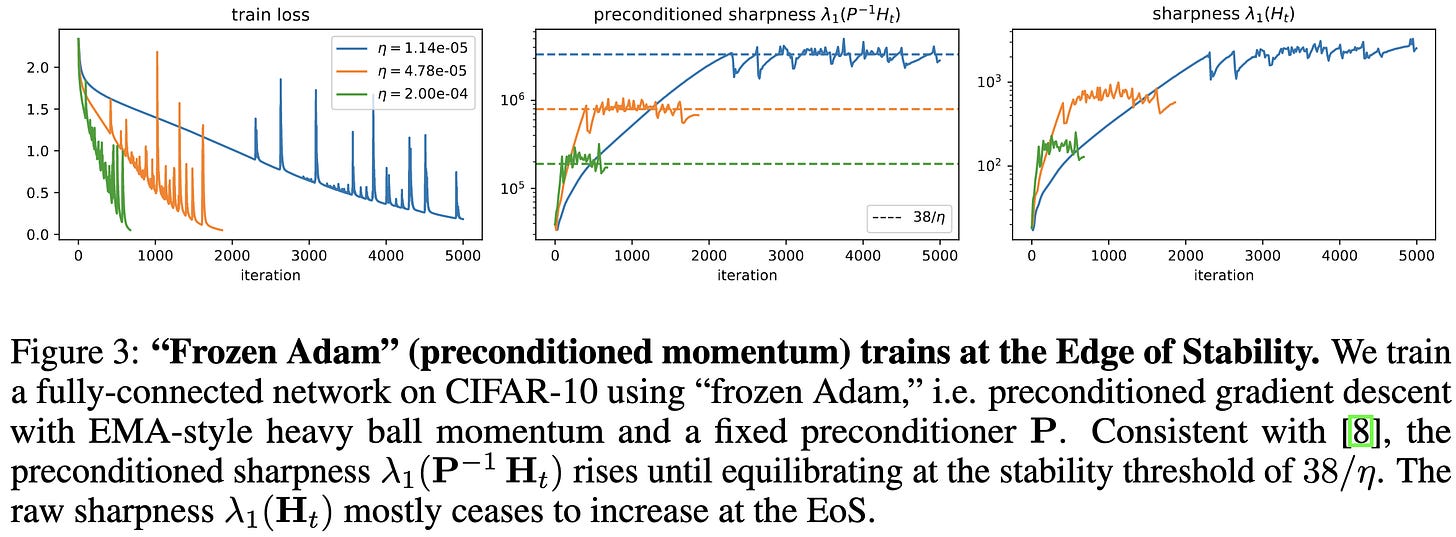
With frozen preconditioning, full-batch Adam plateaus at exactly the sharpness one would expect based on the momentum and learning rate: 38 / lr. This indicates that the adaptive preconditioning is key.
Interestingly, this closed-form sharpness in the full-batch case also happens for other architectures,
as well as other optimizers:
Besides the main finding that you need to look at preconditioned sharpness for Adam, this paper also reinforces my conviction that deep learning isn’t alchemy. It’s still poorly understand in many ways—and there’s a layer of dataset- and model-dependent alchemy on top—but there’s underlying structure governing most of what’s going on.
Language Models Can Teach Themselves to Program Better
To teach models to program, you used to give them a natural language prompt. But recent work has shown that you can instead just show them a unit test and tell them to generate a program that satisfies it (a “programming puzzle”). This is way nicer because it’s simpler and you can just run the code to see if it works.
What this paper proposes to do is use a language model to generate such puzzles, and then use the puzzles to improve the model.
This approach works really well. They find that using generated (puzzle, solution) pairs helps a lot, as does only using pairs where the solution is correct.
This is a clever method and a cool result, but the implications worry me. The Chinchilla paper shows that training data is currently the limiting factor in scaling up language models. But if we can generate unlimited training data for coding in particular, this suggests that future language models will be far better at coding than anything else.
This might be bad because coding ability is the one thing that could make deployed models hard to control—like, no amount of English proficiency lets you modify your own source code or break out of a Docker container. But if you can code at a superhuman level? Who knows how many computers you can infect, how much you can deviate from your original programming, etc.
OLLIE: Derivation-based Tensor Program Optimizer
Let’s say you want to optimize the low-level implementation of your tensor program (i.e., neural network). You can optimize it at the “expression” level (e.g., materalized im2col vs implicit GEMM conv) or the “schedule” level (e.g., loop tiling, shared memory loads/stores).
This paper proposes a method for expanding the expression-level search space of your tensor compiler. By using a guided search over possible rewrites of your overall network, they generate models that run faster once plugged into a back-end schedule optimizer like TVM.
Concretely, they propose a set of “derivation rules” used to transform networks into mathematically equivalent networks that might run faster.
By applying these rules, they sometimes discover unorthodox representations of operators or subnetworks.
After exploring enough alternate expressions, they can discover more efficient approaches than the traditional ones.
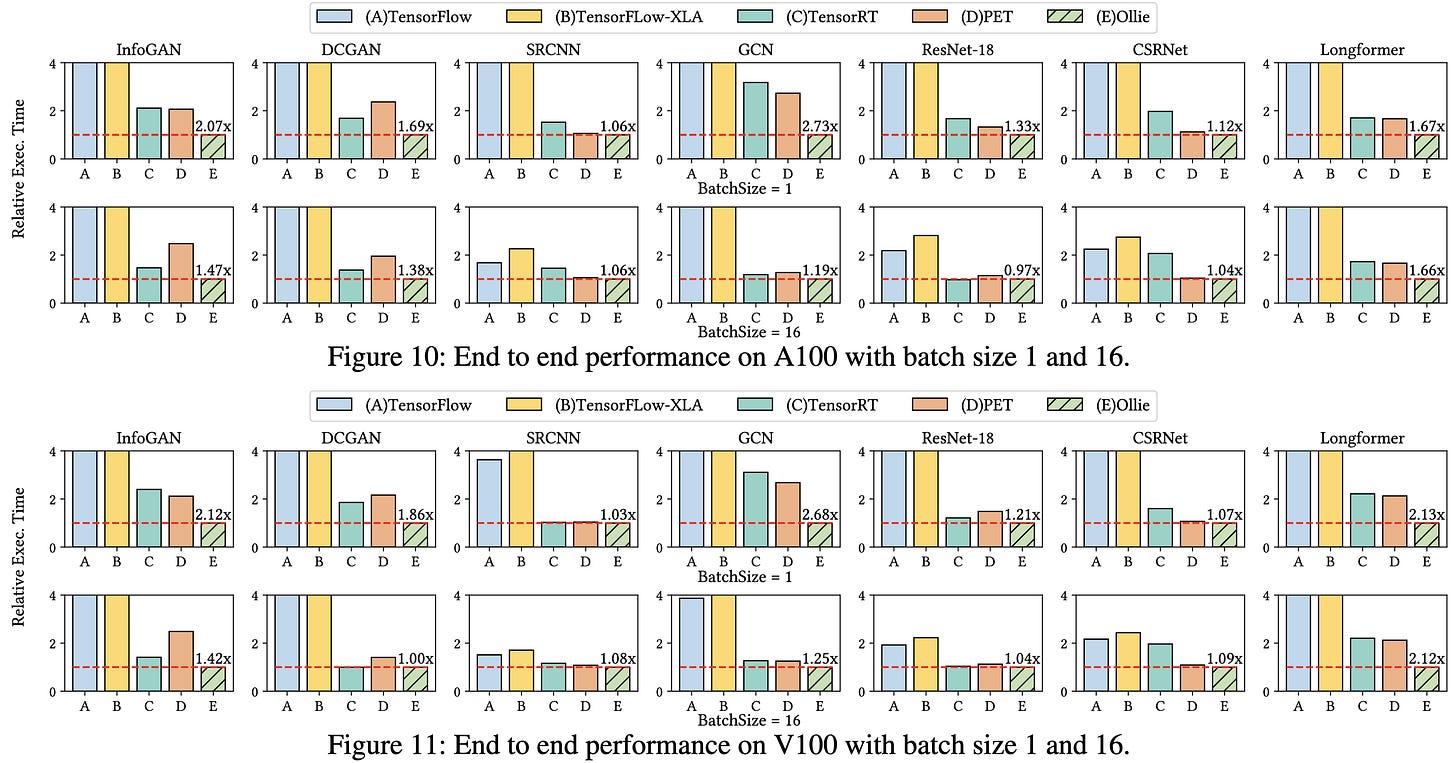
On both A100s and V100s, they obtain significantly lower inference latencies than both raw framework implementations and strong baselines like TensorRT.
There is a time cost to exploring all these different schedules, but it’s small compared to the cost of training the network. And their guided search helps quite a bit compared to brute force search.
There don’t seem to be large returns to further exploration past a certain point.
tl;dr This is a dense systems / programming languages paper that I’d definitely recommend for anyone who cares about tensor compilers.
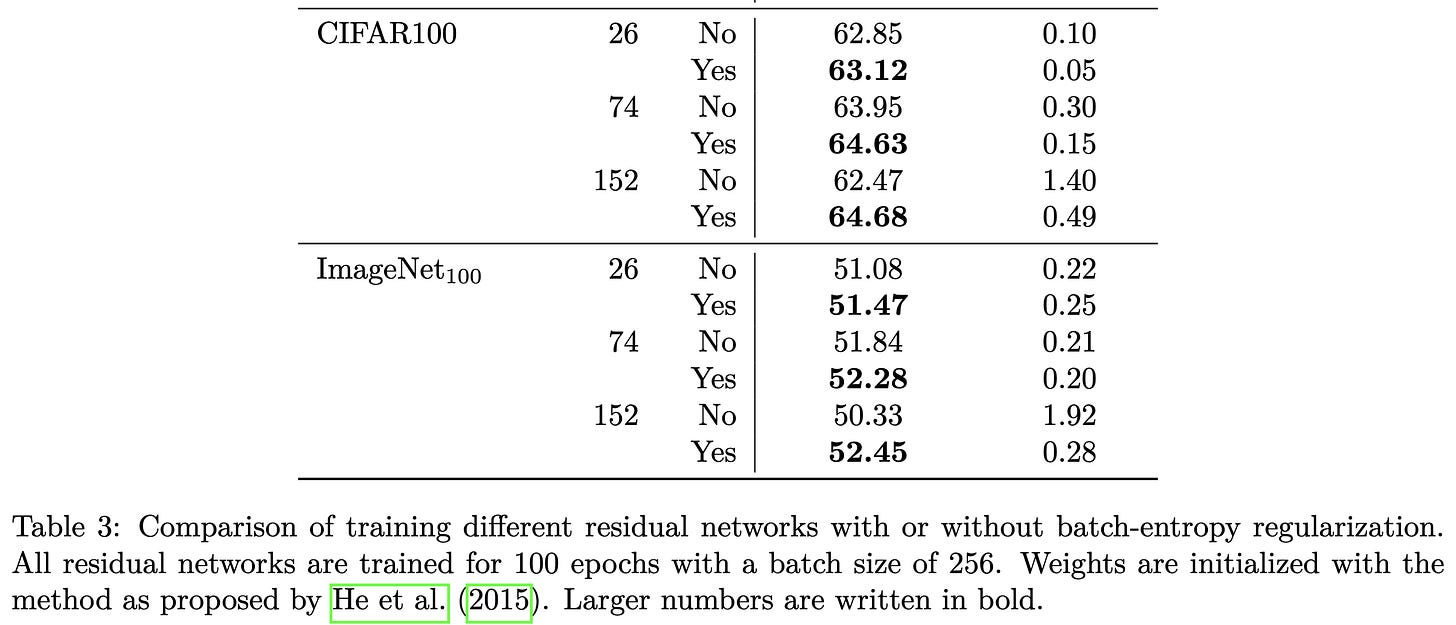
Improving the Trainability of Deep Neural Networks through Layerwise Batch-Entropy Regularization
They apply a penalty to the estimated entropy of each layer to try it make it equal to a learned, layer-specific target value.
They estimate the entropy by assuming each neuron k within each layer l is an independent Gaussian, with standard deviation observed over different samples in the batch.
Instead of just adding their penalty to the cross-entropy loss, they multiply the cross-entropy loss by (1 + their penalty). This makes their penalty only matter when both it and the cross-entropy are large.
They have to tune the a couple hparams, but once they do, they get consistent improvements across various image classification models:
As well as various NLP datasets with BERT variants:
Their penalty also lets vanilla MLPs not fall apart when the depth gets too large. This isn’t that surprising since neuron-level standard deviations are similar to what normalization ops compute. But it is interesting that adding a loss (which has no inference-time overhead) manages to do this.
Dynamic Batch Adaptation
They compute gradients for each tensor for each sample, instead of summed across samples, and select contiguous chunks of these per-sample gradients to keep. Similar to selective backprop, but with selection on a per-layer basis instead of once at the network’s output. They do the selection with one of two greedy algorithms that they randomly choose between.
Their approach seems to let them get away with showing the network less data as evaluated on MNIST.
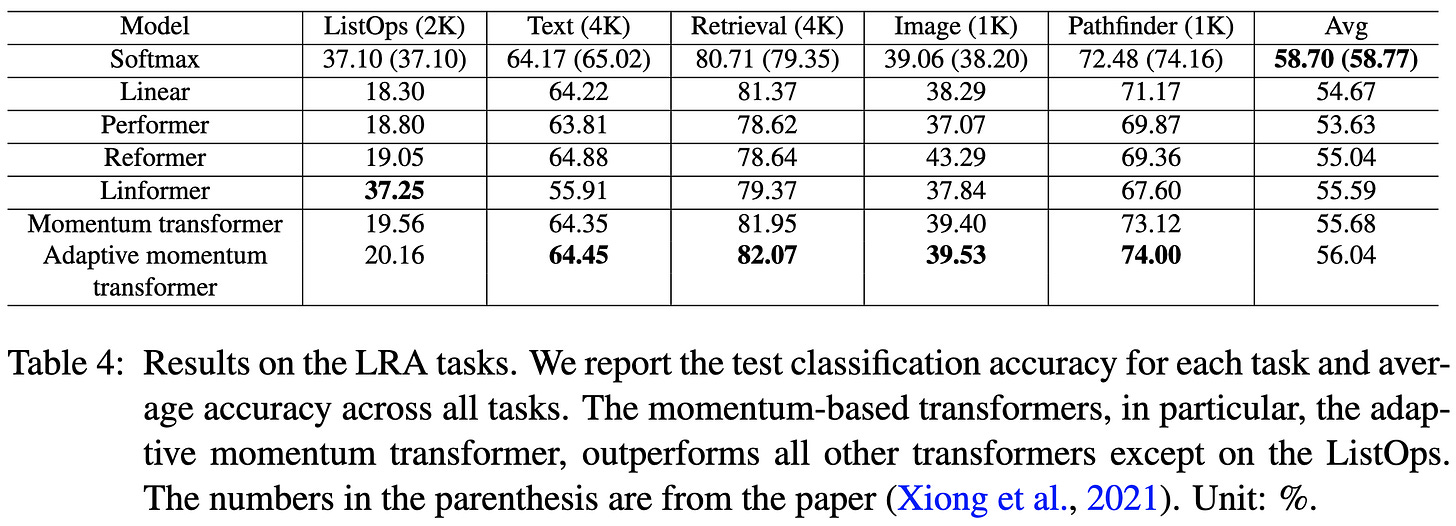
Momentum Transformer: Closing the Performance Gap Between Self-attention and Its Linearization
Linear attention can be thought of as having a shared state that gets updated after each token. What if we added momentum to this state update?
Given hparams γ and β for the step size and momentum, they compute the output vector v_i for each query i as:
This works fine for inference, but is hard to parallelize. For increased training efficiency, they use an equivalent expression during training that allows layerwise parallelism:
They also add momentum to the residual connections, and propose an automatic means of setting the associated momentum parameter based on a local quadratic approximation.
Their method often outperforms various baselines on long-range arena tasks. The “Adaptive Momentum Transformer” is their method including the automatic momentum setting.
These aren’t huge improvements, but what matters is whether their proposed intervention makes a given model better. And that does seem to be the case, making linear transformers more accurate without messing up their speed.
What would really convince me is a plot where they add their momentum mechanism to a variety of linear transformer formulations and show that it consistently helps all of them. But I still like that their method can be understood as a well-defined intervention, rather than a mysterious bag of modules and hparams that supposedly make the numbers go up.
Eco2AI: carbon emissions tracking of machine learning models as the first step towards sustainable AI
They made an open-source Python library for estimating carbon emissions that has more features than similar libraries. Works for both training and inference.
What I found interesting is that they talk about identifying the environmental impact of specific model interventions. E.g., “With the help of eco2AI we
demonstrated that usage of 4-bit GELU decreased equivalent CO2 emissions by about 10%.”
Symmetry Regularization and Saturating Nonlinearity for Robust Quantization
They introduce two training changes to make post-training quantization more effective.
First, they enforce that the distributions of weights in each tensor be symmetric around 0. They do this by sorting all the values, pairing up the k-th highest and k-th lowest weight for all k, and then penalizing the difference in absolute value for each pair. In practice, they use a slightly relaxed version of this.
Second, they run each weight tensor through a tanh before using it in the forward pass. At test time, they get rid of the tanh and just use its output as the weight. This way the weights are differentiable during training but have hard limits for quantization.
Lastly, they train with the ASAM algorithm, since they found that it helps as well; this might be because it encourages flatter minima, in which the loss is less sensitive to weight perturbations.
The results are impressive. Their proposed changes consistently improve the effectiveness of post-training quantization methods compared to vanilla training.
They also improve the effectiveness of LSQ, a quantization-aware training method.
Lastly, they have good ablation studies showing that each of their interventions is beneficial.
I like how systematic the experiments are, plus the modularity of their approach. It’s super easy to drop in a tanh() in as a forward hook, add in SAM to your training, or add another loss term based on the distributions of the weight tensors.
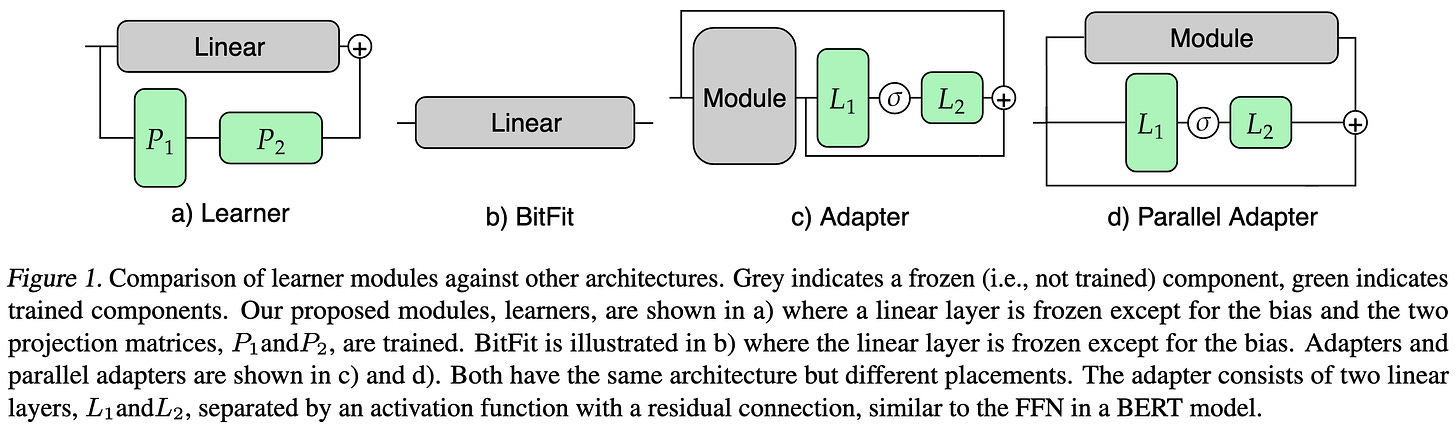
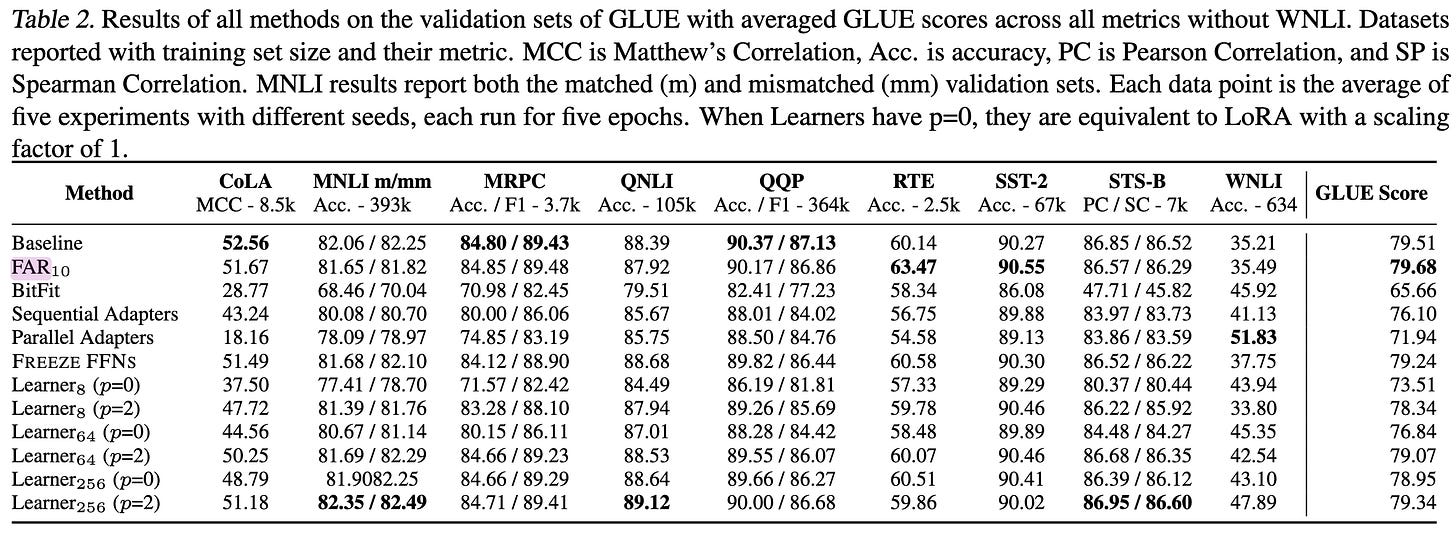
Efficient Fine-Tuning of Compressed Language Models with Learners
They propose to finetune language models by learning a low-rank update to each linear layer. After fine-tuning, these updates can be fused into the linears to avoid adding any overhead.
This method does about as well as other fine-tuning approaches on GLUE.
And has similar runtime and memory consumption:
GTrans: Grouping and Fusing Transformer Layers for Neural Machine Translation
Why do we only use the representation of the last layer instead of some combination of all the internal layers?
This paper proposes to take a subset of the activations from intermediate layers and use a learned combination of them to get an overall representation. Using only the last layer is a special case.
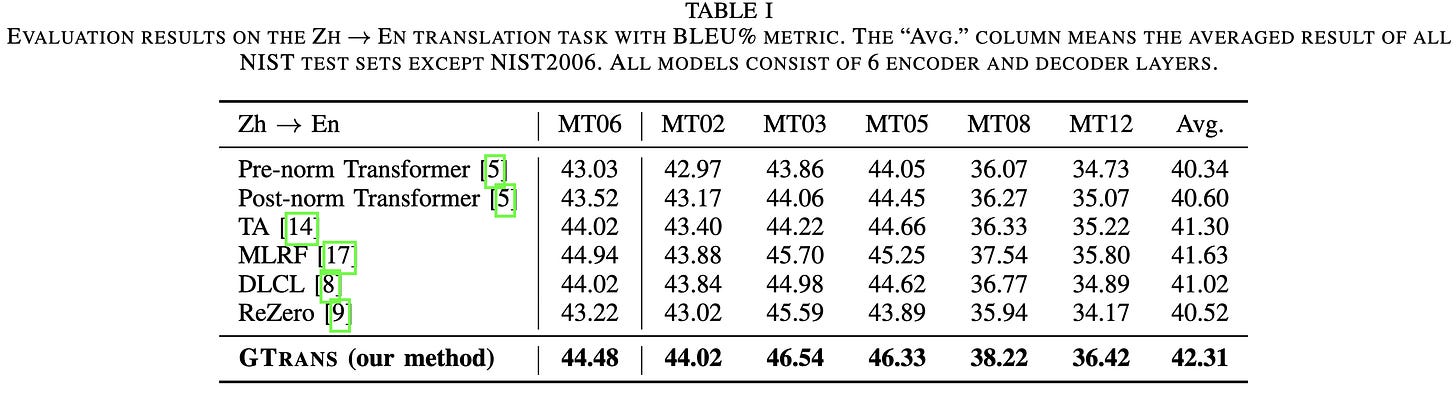
Seems to significantly improve BLEU scores for various translation tasks.
My initial take on this was that it would surely hit memory issues for on-device inference since you’d have to keep around all these old activations. But since they use sigmoids for each layer rather than a softmax, they don’t actually have to keep the old activations—just one tensor they update incrementally. It’s still going to be a memory bandwidth hit, but it might actually be worthwhile given their quality gains.