2022-5-1: PolyLoss, Subquadratic loss landscapes, Large-scale training on spot instances
An Extendable, Efficient and Effective Transformer-based Object Detector
Proposes an object detection approach in the same vein as DETR. There’s a lot of stuff here—a particular neck + head structure, three different types of attention, several loss functions, multi-scale feature map fusion, and more. But they have good results, including tradeoff curves of inference latency vs AP, as well as thorough ablations of different components. Worth digging into if you’re trying to push the limits of object detection (or just turn everything ever into a transformer because it lets you use less competitive baselines).
Schrödinger's FP: Dynamic Adaptation of Floating-Point Containers for Deep Learning Training
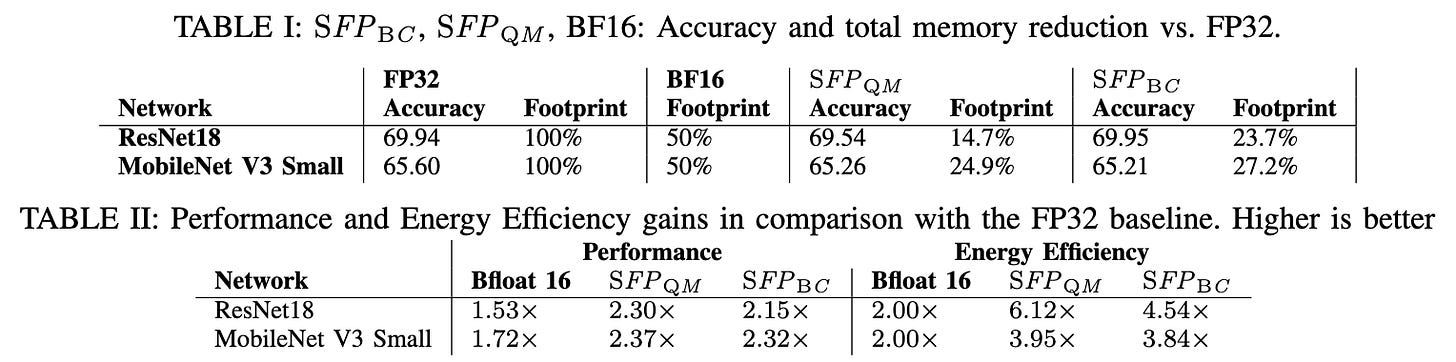
HW/SW codesign paper trying to speed up training through compressing FP numbers intelligently. Two options for compressing mantissa bits: one that tries to get bit length for a given layer differentiable, and one that sets it globally using a loss-based heuristic. They compress exponents by delta coding them and assuming (With some justification) that they follow a normal distribution.
For mantissas, good old straight-through estimator with bitlengths randomly rounded up or down in proportion to a latent variable they differentiate with respect to. Computed separately for weights and activations. Or, as second option, heuristically try to reduce bitwidth until training stops improving the network. Not sure this is really doing more than just picking a decent, fixed value though—e.g., looks like it basically just uses 4 bits all the time with bf16:
Decent results but not super compelling. They definitely get energy and speed gains, but not much that better than bf16 baseline. The heuristic mantissa compression works better than the more complicated differentiable version. Suggests to me that something like bf12 would work—which doesn’t seem too surprising.
It's DONE: Direct ONE-shot learning without training optimization
To add a new class, just take the final embedding for one sample from that class and add it to the final linear classifier as a new column in the weight matrix. Basically a gaussian naive bayes assumption, although they don’t frame it that way.
They don’t really compare to any baselines so I’m not sure whether this approach is a good idea or not. But it certainly is fast, and at the very least might make sense as an initialization scheme.
AutoLossGen: Automatic Loss Function Generation for Recommender Systems
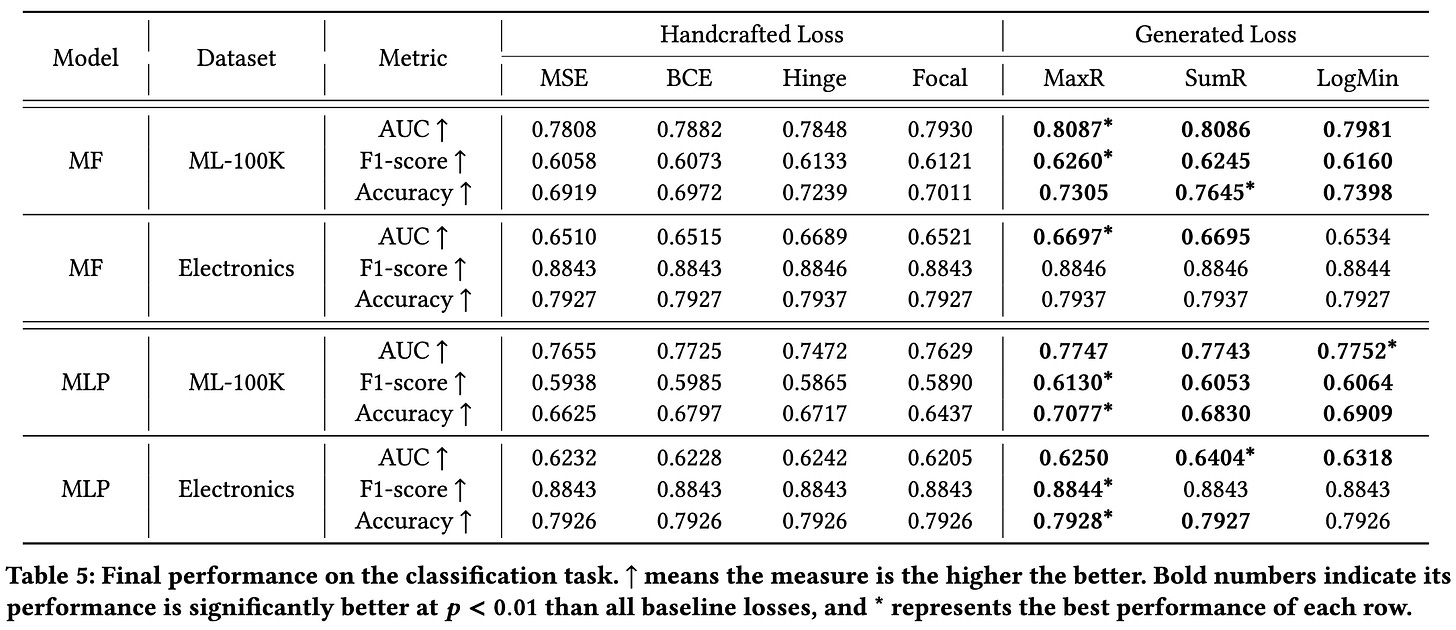
Uses RL to generate a loss function by composing variables and algebraic operations on them. Evaluated on pretty small datasets, but does seem to outperform traditional losses pretty consistently.
⭐ PolyLoss: A Polynomial Expansion Perspective of Classification Loss Functions
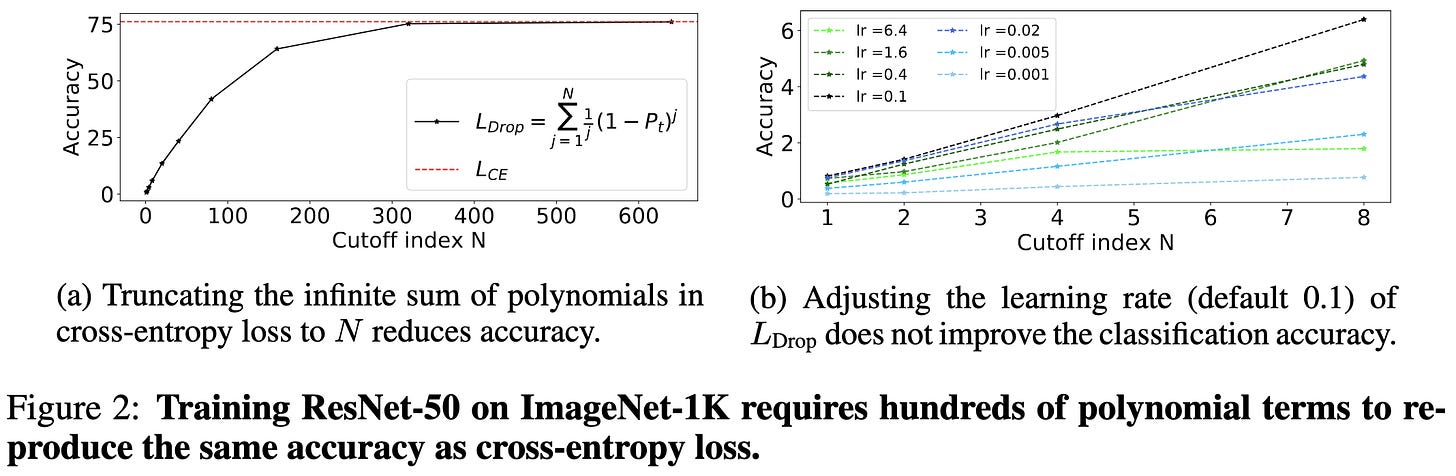
Any reasonable loss function can be expressed as its Taylor expansion, with a fixed coefficient for each polynomial in the infinite series. What we if picked the coefficients intelligently, rather than just using hardcoded values?
Since there are infinitely many such coefficients, they propose to just focus on the lower-order ones. Or even just the very first one (label - prediction)^1. And to make it even simpler, we can consider only positive coefficients. At this point we have a grid-search-able hparam, and it turns out that tuning it can yield ~0.3-0.5% higher accuracy / AP for image classification and detection tasks.
One finding that’s intuitive in retrospect is that the first polynomial coefficient plays a large role early in training (ResNet-50 on ImageNet shown below). This makes sense because, as the model gets more accurate, the higher-order terms go to zero (i.e., we tend to be to the far right of the curve in their figure 1).
In light of that finding, they propose treating the first poly coefficient as a hyperparameter and tuning it. They find that the best coefficient to use varies by task. In fact, image classification works better with larger coefficients than cross-entropy (yielding more confident predictions), while detection works better with smaller coefficients (yielding less confident predictions).
What I really want to know is how this would compose with label smoothing, which tends to have even larger improvements for image classification and be less sensitive to hparams. Also curious because it makes model predictions less confident, which is the opposite of what they found to help.
I’m also not totally sold on this being a worthwhile hparam to introduce since the accuracy gain isn’t that large. Like, there are a million ways I can add an hparam, tune it a lot, and get a small lift. What’s useful is if it’s some mix of an especially large lift or especially easy to tune. I’m hoping that the rest of us can just use their tuned values for classification and detection tasks and get a lift for free, right out of the box.
VICReg: Variance-Invariance-Covariance Regularization for Self-Supervised Learning
I don’t know if if this is SOTA for self-supervised learning, but it sure is elegant. Forces embeddings of two transformed versions of the same image to be similar, but also for the latent representations to vary across images and have close to isotropic covariance. Having to set the weights for the different terms is a little annoying, but feels like an “oh yeah, of course, why didn’t I think of that?” kind of method (in a good way).
Balancing Expert Utilization in Mixture-of-Experts Layers Embedded in CNNs
Applying sparse mixture of experts to ResNet-18 on CIFAR-100. Big tables of negative results; i.e., lower accuracy than baseline model (not to mention MoE overhead). Occasional small improvements for particular expert counts, expert sparsity, and routing approaches, but not really better than I’d expect from multiple hypothesis testing. Makes sense; ResNet-18 is an ImageNet network with a ton of capacity relative to CIFAR-10’s size, so adding even more capacity via MoE is unlikely to help. They also have a lot of visualizations of what different experts are doing (although personally I’m always skeptical of this sort of probing).
⭐ The Multiscale Structure of Neural Network Loss Functions: The Effect on Optimization and Origin
Really interesting paper on empirical loss landscape curvature and its effect on optimization. tl;dr, loss landscapes are subquadratic near minima, at least in their CIFAR-{10,100} experiments. Why does this matter?
This means that instead of having constant curvature, the curvature increases as you move closer to the minimum. First, this implies that quasi-newton methods that construct a local quadratic approximation will systematically take steps that overshoot the minimum. This might explain why using a moving average of your weights is often helpful.
Second, it explains the edge of stability results (which they reproduce) showing that the model tends to reach a point in parameter space where the largest eigenvalue of the hessian is 2 / learning_rate. With increasing curvature as you approach a minimum, the optimization hits a ring where it can’t descend any further, and instead keeps bouncing out because the step size is too large.
They argue that this subquadratic and multi-scale structure emerges naturally from different samples having different scales in parameter space. If you add up a bunch of minima of different widths, you end up with one funky looking and probably subquadratic minimum.
I really like this paper. It focuses on a simple empirical observation that’s intuitive and makes sense of existing results. It also makes me wonder how best to design an optimizer if we know a priori that the loss landscape is subquadratic, rather than quadratic.
Hybridised Loss Functions for Improved Neural Network Generalisation
Shows on some small networks and datasets that using a convex combination of squared error and cross-entropy works better than either alone. This is especially true when you start with the squared error and move to cross-entropy when the accuracy plateaus. Although this approach also has more degrees of freedom than the baselines, so it might just be an artifact of algorithm overfitting.
Automating Neural Architecture Design without Search
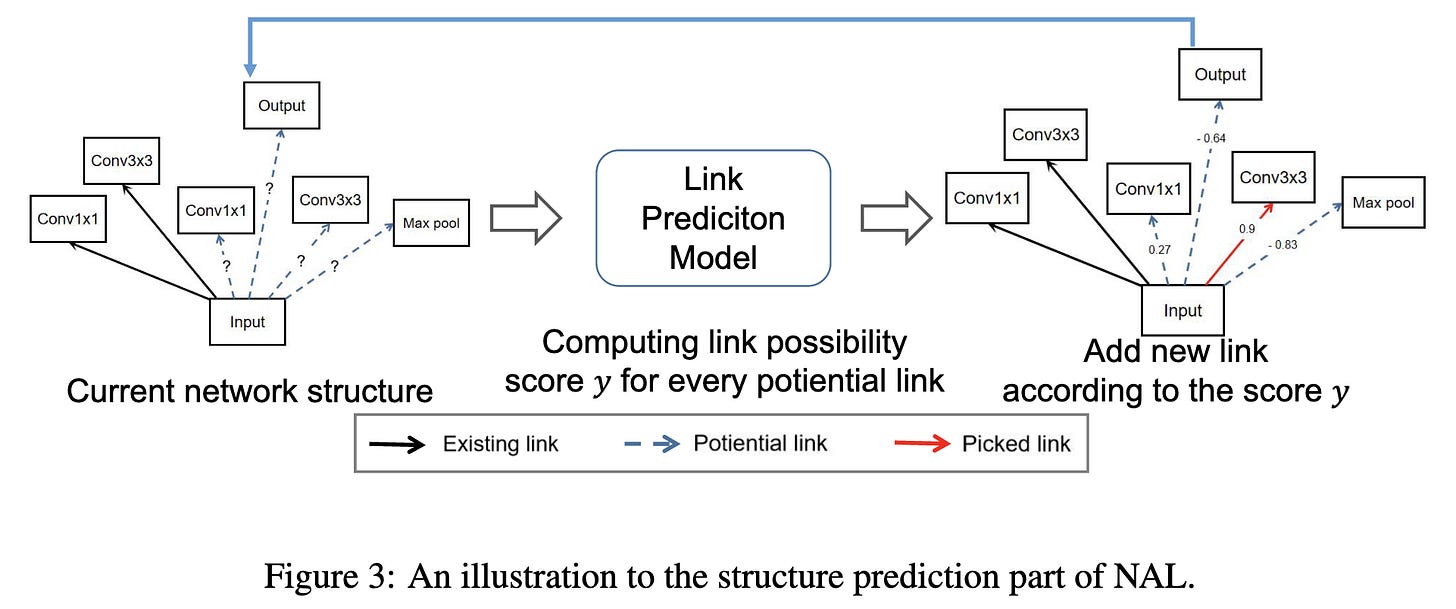
Reportedly outperforms other NAS methods with only 20 seconds of computation. They reduce the problem to that of link prediction in a directed graph.
They extract the 30 highest and lowest accuracy networks on NAS-Bench-101 and preprocess them to get training data. Namely, they treat all the edges in the top networks as positives, the absent edges in the top networks as negatives, and edges in the bottom networks as negatives.
This lets them train a small GNN that can score potential edges. I can’t figure out how they add nodes, but they sample from the softmax of the scores of all potential edges at a given time in order to greedily add edges.
Seems to work really well on both ImageNet and CIFAR-10. Although I am slightly skeptical due to the number of hparams that need to be set; number of vertices, number of edges, number of cells, GNN hparams, etc.
Also works really well on CIFAR-10. One the one hand, CIFAR-10 is a toy problem. On the other hand, 98% accuracy is really hard to do.
Bamboo: Making Preemptible Instances Resilient for Affordable Training of Large DNNs
Trying to facilitate training on spot instances. Assumes pipeline parallelism or pure data parallelism; no support for model parallelism.
I like that they actually recorded real-world preemption patterns. They find that it’s really uncommon to have the full 64 spot instances they requested.
The frequent preemptions result in naive checkpoint-and-restart approaches making slow progress.
System is implemented in ~7kloc on top of deepspeed and torchelastic. They modified deepspeed to do asynchronous checkpointing, which might be independently useful.
Interestingly, their system ignores cloud preemption notices since they don’t always happen on GCP (and are just 30s notice even if they do). Instead they just detect socket timeouts.
Stores an extra copy of the model slice for each pipeline stage in the preceding stage, and also does redundant computation of forward and backward pass for this extra slice. So 2x model storage cost and 2x work done by each node. Though fortunately not 2x communication. 2x compute overhead can sort of be masked by scheduling the computation within pipeline bubbles.
Overall, saves up to 2x money vs on-demand instances when pre-emption rates are low enough (10-20%), though it does run slower.
Seems to significantly outperform Varuna under similar conditions:
Scales down to 8-node pure data-parallel pretty well, though not that much better than just checkpointing and restarting. They have to overprovision nodes by 1.5x to make this work without pipeline parallelism.
Overall, this is probably useful for large scale distributed training on spot instances; in the right situation, it could save you up to 2x training cost in exchange for slower training. This doesn’t feel to me like the optimal way to solve the problem yet, but seems like a well-executed and practical project.
Can deep learning match the efficiency of human visual long-term memory to store object details?
They replicate a classic psych study on some neural nets. Namely, they show the model a long sequence of images and then show it a set of paired images in which only one of the two was in the training set.
Humans are really good at this after even a single exposure to the training set, but it takes neural nets quite a few passes to get the same recognition accuracy.
Unsurprisingly, large pretrained models are better at this.
Overall, I’m not sure what to make of these results. Partially because they only tested Image GPT models, which makes we wonder about the generalizability. But also because I can’t tell at these model sizes and amounts of training data whether this says that humans have a more sample efficient learning algorithm (which would be interesting), or just that human brains are bigger models that have seen more data (which is not interesting).
MAPLE-Edge: A Runtime Latency Predictor for Edge Devices
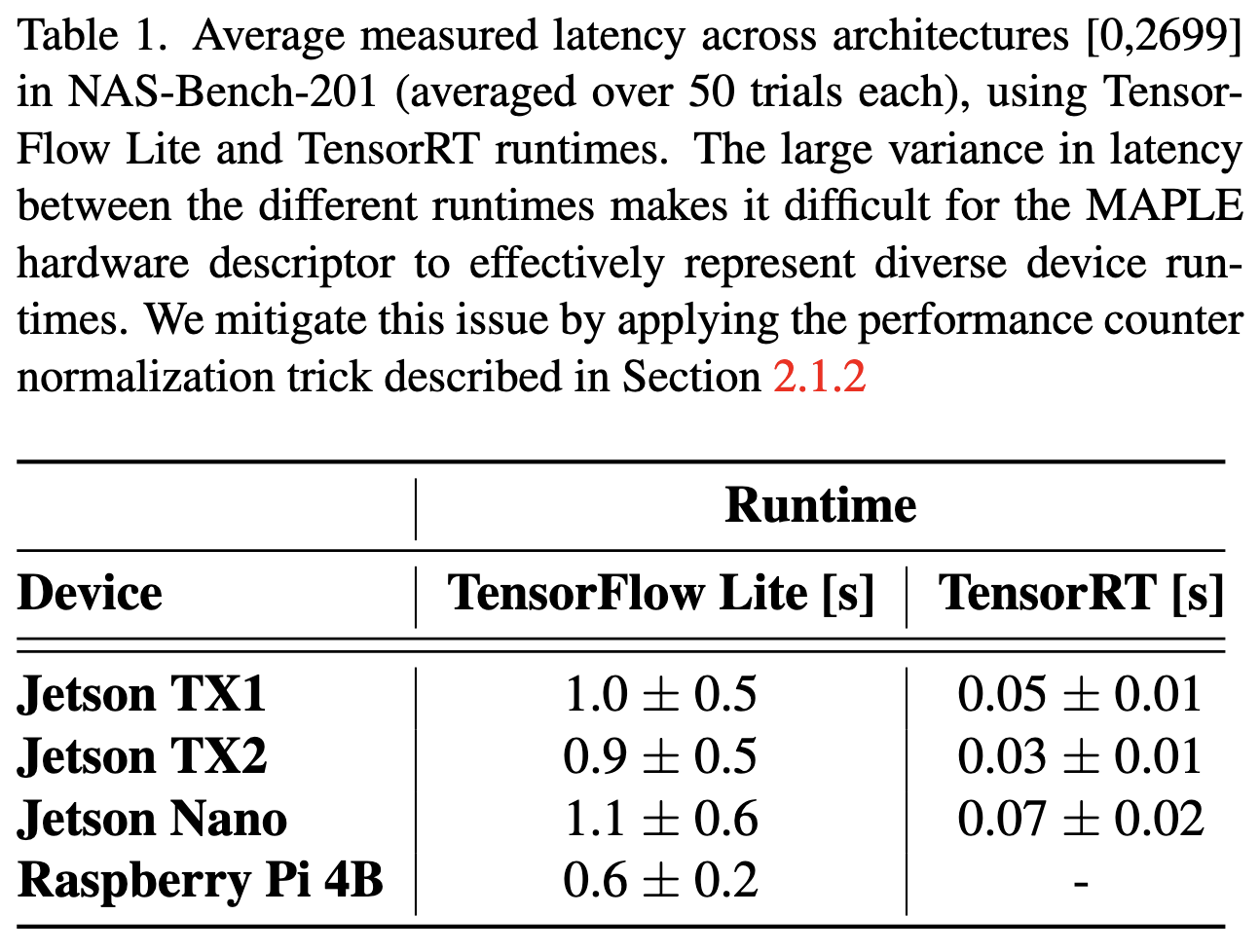
Trying to predict inference latency on edge devices, treating it as a data science problem. They collect a dataset of measured latencies and hardware perf counters for {CPU-cycles, instructions, cache references, cache-misses, L1d loads, and L1d misses} using the 2700 NAS-Bench-201 models running on Jetson devices and RPis. 2 GPU-minutes to train their model. I’m a little confused about their experimental setup and method, largely because they refer to their previous paper (“the seminal MAPLE technique [1]”) for a lot of the details. But my main takeaway is that this is confirmation that predicting neural net latency is a tractable data science problem, even without super complicated feature engineering or a ton of data.
Also, shows that inference latency with TensorRT can different significantly from the latency you would expect from just summing the time taken by each op, thanks to its graph optimizations. Unsurprising, but valuable to see it measured so thoroughly.